с 01.01.2024 по 01.01.2026
Новосибирск, Новосибирская область, Россия
сотрудник с 01.01.2025 по 01.01.2025
Новосибирск, Новосибирская область, Россия
УДК 550.8 Прикладная геология и геофизика. Геологические методы поисков и разведки, интерпретация их результатов
ГРНТИ 38.57 Методы поисков и разведки месторождений полезных ископаемых
ОКСО 05.04.01 Геология
ББК 2 ЕСТЕСТВЕННЫЕ НАУКИ
ТБК 6 ЕСТЕСТВЕННЫЕ НАУКИ. МАТЕМАТИКА
BISAC SCI030000 Earth Sciences / Geography
BISAC SCI032000 Physics / Geophysics
Сейсмическая инверсия является ключевым инструментом количественного прогноза, традиционно используемым для получения акустического импеданса (AI) и соотношения скоростей волн (Vp/Vs). Однако в карбонатных толщах возникают особенности, требующие специализированных подходов. В работе авторами предлагается использовать синхронную инверсию с получением параметров Ламе (λ, μ) и плотности как более информативный инструмент для таких разрезов. Применительно к данным Оренбургской области такой подход обеспечил значительный прирост информативности инверсии по сравнению с классической постановкой (AI, Vp/Vs): коэффициенты корреляции для модулей λ и μ со скважинными данными составили от 0.80 до 0.89, тогда как для AI и Vp/Vs эти значения варьировались от 0.61 до 0.77.
сейсмическая инверсия, параметры Ламе, петрофизические шаблоны, количественный прогноз, аппроксимация Грея
Введение
В последние годы для изучения геологических объектов активно развиваются методы количественной интерпретации, в частности сейсмическая инверсия — технология восстановления упругих параметров горных пород из сейсмических данных. Особую актуальность сейсмическая инверсия приобретает при изучении карбонатных коллекторов, поскольку они содержат значительную часть мировых запасов углеводородов. Однако именно в условиях карбонатных толщ задача инверсии становится особенно сложной [1]. Слабая контрастность упругих свойств делает результат крайне чувствительным к выбору параметризации и инверсионного подхода.
Широкое распространение в мировой практике анализа карбонатных коллекторов получил так называемый LMR-подход (Lambda-Mu-Rho), основанный на исследовании кроссплотов параметров
В настоящей работе выполнена синхронная инверсия сейсмических данных с получением параметров Ламе по аппроксимации Грея. Рассмотрена устойчивость решения обратной задачи в пределах карбонатного разреза и проанализирована применимость восстановленных параметров для прогнозирования распространения коллекторов на примере материалов по участку в пределах Рубежинского прогиба (Оренбургская область). В результате упругие компоненты
Теория и метод
Рассмотрим две изотропные полусферы, имеющие плоскую поверхность контакта, на которую падает плоская продольная волна. Первая полусфера характеризуется свойствами {
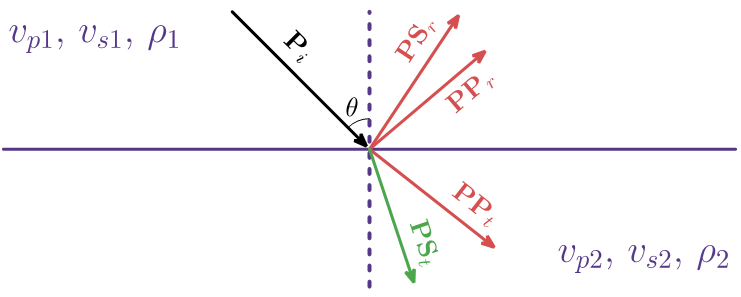
Рисунок 1. Схема отражения и прохождения при наклонном падении продольной волны на границу раздела двух сред
Углы падения, отражения и прохождения на границе для всех волн определяются законом Снеллиуса:
(1)
Коэффициенты отражения и прохождения
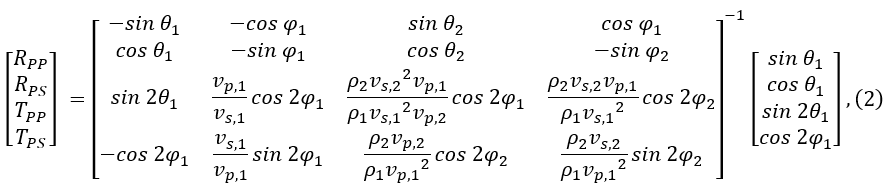
где
Уравнения нелинейны относительно входных параметров и сложны для интерпретации. В силу этого их прямое использование в интерпретации до сих пор остается весьма ограниченным. Компромиссным решением, легко вычисляемым и интерпретируемым, стало применение широкого семейства линеаризованных аппроксимаций этих уравнений. Общий принцип их построения следующий: строится линейная комбинация нескольких переменных в зависимости от параметризации:
(3)
где
(4)
где
В таблице 1 приведены наиболее распространенные линеаризации уравнения Кнота — Цеппритца (
Таблица 1. Линеаризованные аппроксимации уравнения Кнота — Цеппритца
|
|
|
|
|
|
|
|
|
Аки — Ричардс, 1980 |
|
|
||||
|
Фатти, 1994 |
|
|||||
|
Грей, 1999 |
|
|
||||
|
Грей, 2002 |
|
|||||
|
Шуэ, 2002 |
|
|
|
Используя описанные выше способы прямого моделирования, задачу сейсмической синхронной инверсии можно сформулировать так:
(5)
где
В работе исследуется решение задачи инверсии в аппроксимации Грея. Аппроксимация Грея, предложенная в 1999 году (таб. 1), позволяет сформулировать уравнение Цеппритца в контексте фундаментальных параметров волнового уравнения —
В контексте карбонатных пород петрофизический шаблон
Расчет инверсии и последующая интерпретация ее результатов выполнены в программном модуле количественной интерпретации данных сейсморазведки VersaBox, разрабатываемым коллективом Новосибирского государственного университета (НГУ) [9]. Выполнены упругая синхронная инверсия и классификация ее результатов на литотипы «коллектор»/«неколлектор» методом Random Forest [10].
Геологическая характеристика района и используемый комплекс данных
Район исследований расположен в пределах Рубежинского прогиба (южная часть Бузулукской впадины) на территории Оренбургской области. В тектоническом плане территория характеризуется развитой сетью разломов и значительной мощностью осадочного чехла. Исследования сфокусированы на отложениях каменноугольного и девонского возраста, которые залегают на глубинах до 4700 м.
Литологически изучаемый интервал представлен сочетанием карбонатных и терригенных толщ. В карбонатной части разреза присутствуют как толщи, сложенные рифогенными постройками, так и пласты плотных известняков с зонами развития кавернозно-пористых, вторичных трещиноватых доломитов вблизи разломов [11]. В меньшей степени в разрезе присутствуют также терригенные отложения, в том числе с наличием клиноформных комплексов [12].
В основу исследования положен комплекс геофизических данных, включающий:
-
набор из пяти частично-кратных сейсмических сумм, охватывающих диапазоны: 0–8°, 6–14°, 12–20°, 18–26° и 24–35°;
-
комплекс ГИС (геофизических исследований скважин) по пяти скважинам, включающий кривые широкополосного акустического и гамма-гамма плотностного каротажей.
Традиционно для обоснования проведения сейсмической инверсии принято предварительно рассматривать разделение литотипов в поле упругих параметров [13]. Такой анализ проводится по данным ГИС в изучаемом интервале разреза.
В рамках статьи в качестве примера детальной интерпретации был выбран интервал, который включает в себя карбонатные отложения эйфельского яруса (бийско-афонинская толща). Наличие коллектора в них принято связывать с трещиноватыми и кавернозными зонами, обусловленными гидротермальной доломитизацией [14].
На кроссплотах, отражающих влияние степени доломитизации известняка на значения упругих параметров (рис. 2), видно, что функции плотности вероятности литотипов известняк-доломит формируют частично пересекающиеся области, однако при этом все-таки прослеживается ряд закономерностей. В интервалах с более высокой доломитизацией наблюдаются повышенные значения модуля
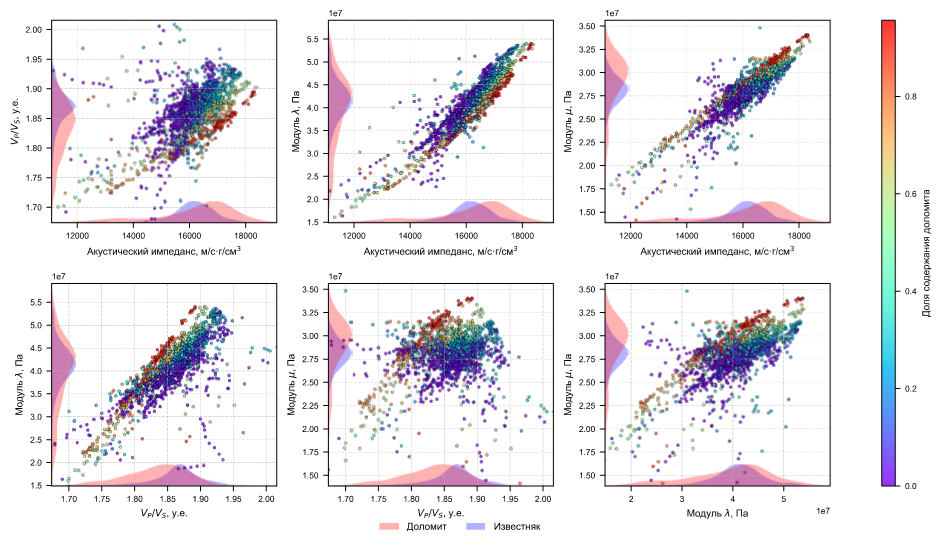
Рисунок 2. Зависимости упругих свойств для бийско-афонинской толщи разреза. Цветом показано изменение объемного содержания доломита. На осях нанесены функции плотности вероятности для литотипов доломит (красный) и известняк (синий)
Несмотря на неоднозначность распределений, параметр
Результаты
С использованием описанных данных проведена синхронная инверсия в аппроксимации Грея.
Для контроля качества (quality control, QC) результатов инверсии сейсмических данных было проведено сравнение расчетных упругих параметров с данными ГИС, приведенными к сейсмической полосе частот (рис. 3). Параметризация на основе аппроксимации Грея позволила получить решение, адекватно описывающее геологическую среду. Алгоритм показал устойчивые результаты в интервале, где создается резкий контраст упругих свойств за счет смены терригенных и карбонатных пород. Важно отметить, что эта устойчивость решения сохраняется даже в пределах карбонатных интервалов (указаны на рис. 3 красными стрелками), для которых характерно присутствие рифовых построек в разрезе и которые описываются низким контрастом упругих свойств. Количественная оценка точности по скважинным данным показала высокую степень соответствия: значения коэффициентов корреляции для параметров
Также был применен традиционный подход инверсии с восстановлением
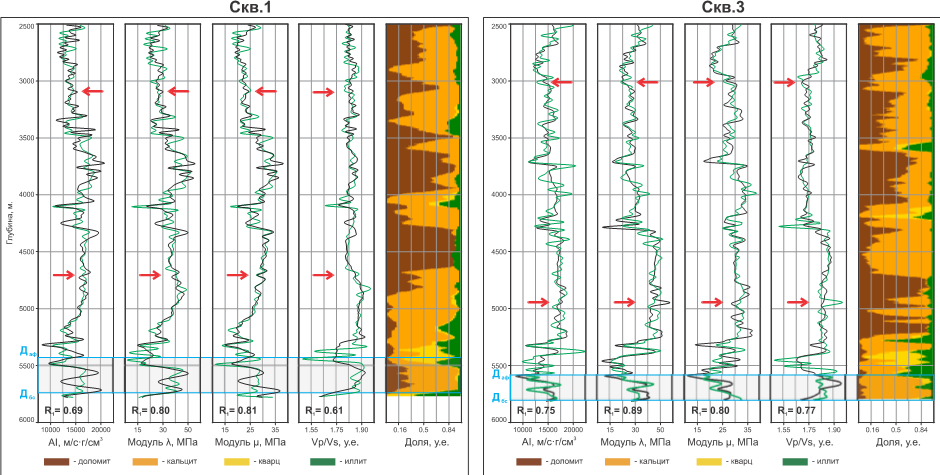
Рисунок 3. Планшеты результатов классической и LMR сейсмических инверсий для скв. 1 и скв. 3: кривые ГИС обозначены черным, кривые инверсии обозначены зеленым. Цветное изображение представляет из себя объемную минералогическую модель с относительным содержанием минеральных компонентов
Объемный прогноз зон вероятного развития коллектора результатов инверсии был выполнен с использованием алгоритма Random Forest, где в качестве признаков модели применены инверсионные параметры Ламе.
На рисунке 4 показан разрез прогнозного куба, отражающий вероятностное распределение коллектора в пределах карбонатов эйфельского яруса. Также на рисунке 4 показан в качестве примера разрез одного из восстановленных в результате синхронной инверсии упругих параметров —
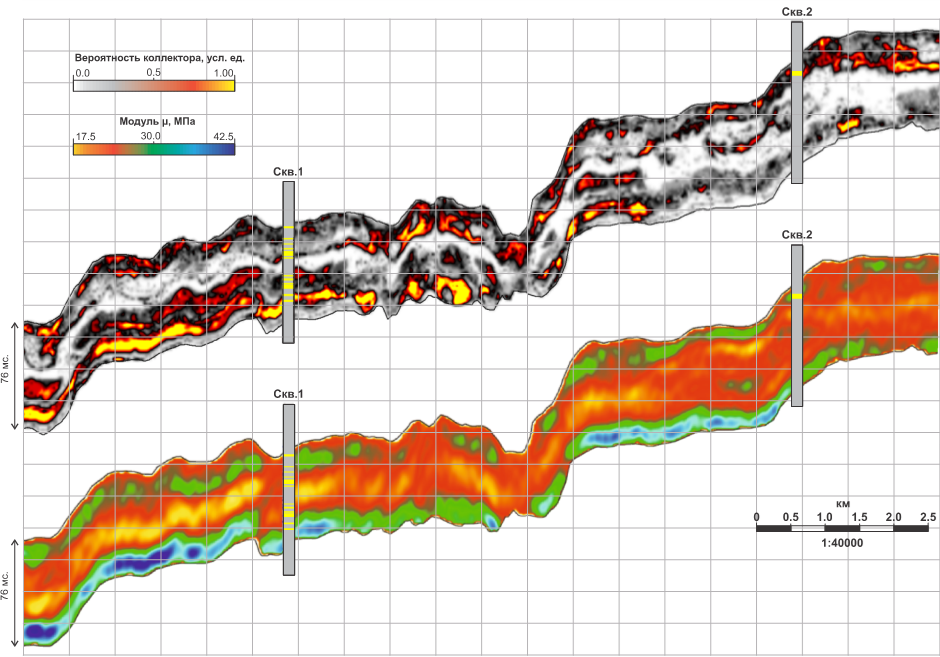
Рисунок 4. Интервал эйфельских карбонатов (бийско-афонинская толща). На верхнем разрезе показан прогноз распространения коллектора по результатам LMR-инверсии. Нижний разрез представляет разрез модуля
Совместный анализ восстановленных параметров Ламе и результата прогноза распространения коллектора, полученного с помощью алгоритма машинного обучения, показывает, что использование
Выводы
Проведенные исследования показали высокую информативность LMR сейсмической инверсии при анализе карбонатных разрезов. Для данных Оренбургской области результаты такой инверсии продемонстрировали высокую согласованность с данными ГИС: коэффициенты корреляции между восстановленными модулями
Совместное использование инверсии в параметризации Грея и алгоритма Random Forest способствовало выделению зон с повышенной вероятностью развития коллектора.
Таким образом, LMR-инверсия может рассматриваться как перспективный инструмент анализа слабоконтрастных карбонатных разрезов, расширяющий возможности существующих подходов к интерпретации сейсмических данных.
Благодарности
Авторы выражают глубокую признательность д. ф.-м. н. Г. М. Митрофанову, к. ф.-м. н. А. А. Дучкову за координацию исследований. Отдельная благодарность коллективу разработки программного модуля VersaBox за предоставленный доступ к инструментам динамической интерпретации, а также коллективу «Газпромнефть НТЦ» за плодотворное сотрудничество. Работа была выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации (проект № FSUS-2025-0015).
1. Фагерева В. А. Расширение возможностей синхронной инверсии в карбонатах с использованием седиментологического концепта // PROНЕФТЬ. Профессионально о нефти. — 2023. — Т. 8. — № 4. — С. 115–120. — https://doi.org/10.51890/2587-7399-2023-8-4-115-120.
2. Goodway B. Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters / B. Goodway, T. Chen, J. Downton // 67th Annual International Meeting, SEG: Expanded Abstracts. — Dallas, 1997. — Pp. 183–186.
3. Gray F. D. Case histories. Inversion for rock properties / F. D. Gray, E. A. Andersen // 62nd EAGE Conference & Exhibition. — Glasgow, 2000.
4. Urosevic M. LMR. A robust reservoir properties indicator in carbonate reservoirs / M. Urosevic, S. Amiri Besheli, S. S. Hendi, J. Vali // 66th EAGE Conference & Exhibition. — Paris, 2004.
5. Reza M. F. Carbonate reservoir characterization using simultaneous inversion in field “X” / M. F. Reza, M. S. Rosid, M. W. Haidar // AIP Conference Proceedings. — 2019. — Vol. 2168. — https://doi.org/10.1063/1.5132450.
6. Воскресенский Ю. Н. Изучение изменений амплитуд сейсмических отражений для поисков и разведки залежей углеводородов / Воскресенский Ю. Н. — Москва: РГУ нефти и газа им. И. М. Губкина, 2001.
7. Aki K. Quantitative Seismology / Aki K., Richards P. G. — San Francisco: W. H. Freeman, 1980.
8. Oldenburg D. W. Recovery of the acoustic impedance from reflection seismograms / Oldenburg D. W., Scheuer T., Levy S. // Geophysics. — 1983. — Vol. 48. — № 10. — Pp. 1318–1337.
9. Корчуганов В. Д. Simultaneous VersaBox — программный комплекс амплитудной синхронной сейсмической инверсии / Корчуганов В. Д., Побежимов Е. А // Свидетельство о государственной регистрации программы для ЭВМ № 2025611730. — 2024.
10. Breiman L. Random forests / Breiman L. // Machine Learning. — 2001. — Vol. 45. — № 1. — Pp. 5–32.
11. Вилесов А. П. Верхнепалеозойские рифовые системы Рубежинского прогиба (южная часть Бузулукской впадины) / Вилесов А. П., Леденев В. С., Солодов Д. В., Филичев А. В., Богомолова Н. В., Макарова Л. И., Гребенкина Н. Ю., Казачкова А. Г., Сидубаев А. С. // PROНЕФТЬ. Профессионально о нефти. — 2021. — Т. 6. — № 3. — С. 30–42. — https://doi.org/10.51890/2587-7399-2021-6-3-30-42.
12. Гребенкина Н. Ю. Воробьевский терригенный комплекс западной части Рубежинского прогиба: новые данные об особенностях строения и перспективах нефтегазоносности. / Гребенкина Н. Ю., Екименко А. В., Вилесов А. П., Леденев В. С., Сидубаев А. С. // Санкт-Петербург 2023. Геонауки: время перемен, время перспектив. — Санкт-Петербург, 2023. — С. 35–38.
13. Bacon M. Seismic amplitude: an interpreter’s handbook. / Bacon M., Simm R. — Cambridge: Cambridge University Press, 2014.
14. Вилесов А. П. Генезис доломитовых коллекторов бийско-афонинской карбонатной толщи Оренбургской области/ Вилесов А. П., Чертина К. Н., Воронцов И. П., Девятка Н. П. // Геология, геофизика и разработка нефтяных и газовых месторождений. — 2014. — № 11. — С. 25–34.







