employee from 01.01.2024 to 01.01.2025
Novosibirsk, Novosibirsk, Russian Federation
employee from 01.01.2025 to 01.01.2025
Novovsibirsk, Novosibirsk, Russian Federation
VAK Russia 1.6
VAK Russia 1.2.1
VAK Russia 1.2.2
UDC 550.8
CSCSTI 38.57
Russian Classification of Professions by Education 05.04.01
Russian Library and Bibliographic Classification 2
Russian Trade and Bibliographic Classification 6
BISAC SCI030000 Earth Sciences / Geography
BISAC SCI032000 Physics / Geophysics
Seismic inversion is a key quantitative forecasting tool that is traditionally employed to derive acoustic impedance (AI) and the P- to S-wave velocity ratio (Vp/Vs). However, carbonate formations exhibit a range of geological and petrophysical complexities that require specialized approaches. In this study, the authors propose simultaneous inversion for retrieving the Lamé parameters (λ, μ) and density as a more informative technique for such intervals. Applied to seismic data from the Orenburg region, this approach provided a substantial increase in inversion informativeness compared with the classical parameterization (AI, Vp/Vs): correlation coefficients between the derived λ and μ attributes and well data ranged from 0.80 to 0.89, whereas those for AI and Vp/Vs varied from 0.61 to 0.77.
seismic inversion, Lame parameters, rock physics templates, quantitative forecast, Gray approximation.
Введение
В последние годы для изучения геологических объектов активно развиваются методы количественной интерпретации, в частности сейсмическая инверсия — технология восстановления упругих параметров горных пород из сейсмических данных. Особую актуальность сейсмическая инверсия приобретает при изучении карбонатных коллекторов, поскольку они содержат значительную часть мировых запасов углеводородов. Однако именно в условиях карбонатных толщ задача инверсии становится особенно сложной [1]. Слабая контрастность упругих свойств делает результат крайне чувствительным к выбору параметризации и инверсионного подхода.
Широкое распространение в мировой практике анализа карбонатных коллекторов получил так называемый LMR-подход (Lambda-Mu-Rho), основанный на исследовании кроссплотов параметров
В настоящей работе выполнена синхронная инверсия сейсмических данных с получением параметров Ламе по аппроксимации Грея. Рассмотрена устойчивость решения обратной задачи в пределах карбонатного разреза и проанализирована применимость восстановленных параметров для прогнозирования распространения коллекторов на примере материалов по участку в пределах Рубежинского прогиба (Оренбургская область). В результате упругие компоненты
Теория и метод
Рассмотрим две изотропные полусферы, имеющие плоскую поверхность контакта, на которую падает плоская продольная волна. Первая полусфера характеризуется свойствами {
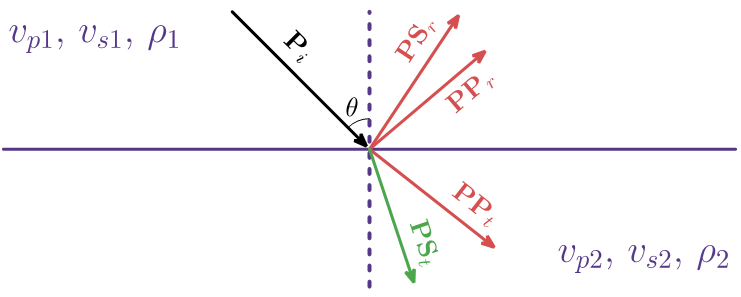
Рисунок 1. Схема отражения и прохождения при наклонном падении продольной волны на границу раздела двух сред
Углы падения, отражения и прохождения на границе для всех волн определяются законом Снеллиуса:
(1)
Коэффициенты отражения и прохождения
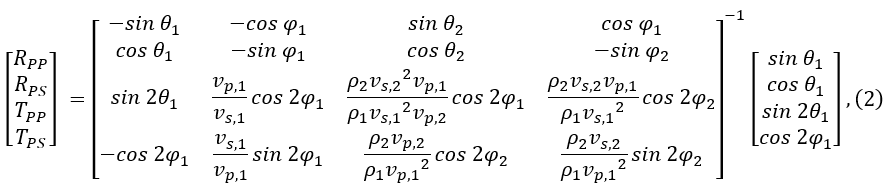
где
Уравнения нелинейны относительно входных параметров и сложны для интерпретации. В силу этого их прямое использование в интерпретации до сих пор остается весьма ограниченным. Компромиссным решением, легко вычисляемым и интерпретируемым, стало применение широкого семейства линеаризованных аппроксимаций этих уравнений. Общий принцип их построения следующий: строится линейная комбинация нескольких переменных в зависимости от параметризации:
(3)
где
(4)
где
В таблице 1 приведены наиболее распространенные линеаризации уравнения Кнота — Цеппритца (
Таблица 1. Линеаризованные аппроксимации уравнения Кнота — Цеппритца
|
|
|
|
|
|
|
|
|
Аки — Ричардс, 1980 |
|
|
||||
|
Фатти, 1994 |
|
|||||
|
Грей, 1999 |
|
|
||||
|
Грей, 2002 |
|
|||||
|
Шуэ, 2002 |
|
|
|
Используя описанные выше способы прямого моделирования, задачу сейсмической синхронной инверсии можно сформулировать так:
(5)
где
В работе исследуется решение задачи инверсии в аппроксимации Грея. Аппроксимация Грея, предложенная в 1999 году (таб. 1), позволяет сформулировать уравнение Цеппритца в контексте фундаментальных параметров волнового уравнения —
В контексте карбонатных пород петрофизический шаблон
Расчет инверсии и последующая интерпретация ее результатов выполнены в программном модуле количественной интерпретации данных сейсморазведки VersaBox, разрабатываемым коллективом Новосибирского государственного университета (НГУ) [9]. Выполнены упругая синхронная инверсия и классификация ее результатов на литотипы «коллектор»/«неколлектор» методом Random Forest [10].
Геологическая характеристика района и используемый комплекс данных
Район исследований расположен в пределах Рубежинского прогиба (южная часть Бузулукской впадины) на территории Оренбургской области. В тектоническом плане территория характеризуется развитой сетью разломов и значительной мощностью осадочного чехла. Исследования сфокусированы на отложениях каменноугольного и девонского возраста, которые залегают на глубинах до 4700 м.
Литологически изучаемый интервал представлен сочетанием карбонатных и терригенных толщ. В карбонатной части разреза присутствуют как толщи, сложенные рифогенными постройками, так и пласты плотных известняков с зонами развития кавернозно-пористых, вторичных трещиноватых доломитов вблизи разломов [11]. В меньшей степени в разрезе присутствуют также терригенные отложения, в том числе с наличием клиноформных комплексов [12].
В основу исследования положен комплекс геофизических данных, включающий:
-
набор из пяти частично-кратных сейсмических сумм, охватывающих диапазоны: 0–8°, 6–14°, 12–20°, 18–26° и 24–35°;
-
комплекс ГИС (геофизических исследований скважин) по пяти скважинам, включающий кривые широкополосного акустического и гамма-гамма плотностного каротажей.
Традиционно для обоснования проведения сейсмической инверсии принято предварительно рассматривать разделение литотипов в поле упругих параметров [13]. Такой анализ проводится по данным ГИС в изучаемом интервале разреза.
В рамках статьи в качестве примера детальной интерпретации был выбран интервал, который включает в себя карбонатные отложения эйфельского яруса (бийско-афонинская толща). Наличие коллектора в них принято связывать с трещиноватыми и кавернозными зонами, обусловленными гидротермальной доломитизацией [14].
На кроссплотах, отражающих влияние степени доломитизации известняка на значения упругих параметров (рис. 2), видно, что функции плотности вероятности литотипов известняк-доломит формируют частично пересекающиеся области, однако при этом все-таки прослеживается ряд закономерностей. В интервалах с более высокой доломитизацией наблюдаются повышенные значения модуля
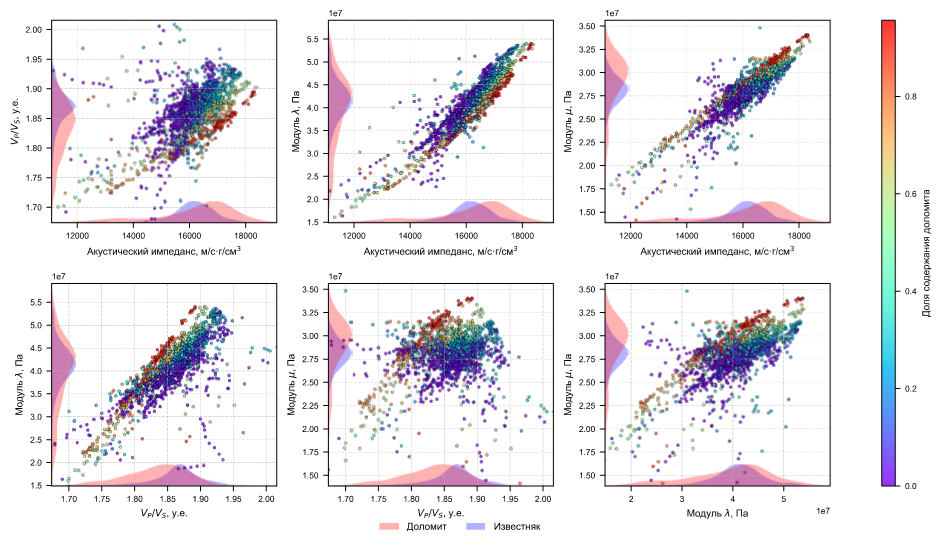
Рисунок 2. Зависимости упругих свойств для бийско-афонинской толщи разреза. Цветом показано изменение объемного содержания доломита. На осях нанесены функции плотности вероятности для литотипов доломит (красный) и известняк (синий)
Несмотря на неоднозначность распределений, параметр
Результаты
С использованием описанных данных проведена синхронная инверсия в аппроксимации Грея.
Для контроля качества (quality control, QC) результатов инверсии сейсмических данных было проведено сравнение расчетных упругих параметров с данными ГИС, приведенными к сейсмической полосе частот (рис. 3). Параметризация на основе аппроксимации Грея позволила получить решение, адекватно описывающее геологическую среду. Алгоритм показал устойчивые результаты в интервале, где создается резкий контраст упругих свойств за счет смены терригенных и карбонатных пород. Важно отметить, что эта устойчивость решения сохраняется даже в пределах карбонатных интервалов (указаны на рис. 3 красными стрелками), для которых характерно присутствие рифовых построек в разрезе и которые описываются низким контрастом упругих свойств. Количественная оценка точности по скважинным данным показала высокую степень соответствия: значения коэффициентов корреляции для параметров
Также был применен традиционный подход инверсии с восстановлением
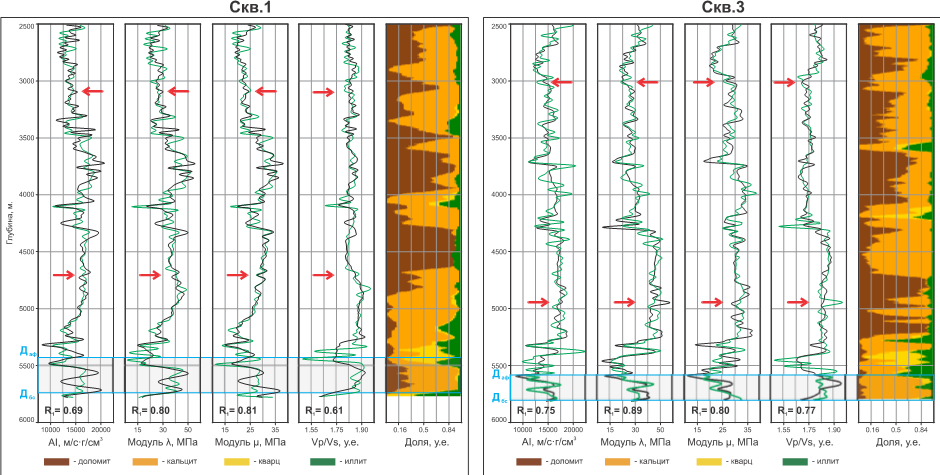
Рисунок 3. Планшеты результатов классической и LMR сейсмических инверсий для скв. 1 и скв. 3: кривые ГИС обозначены черным, кривые инверсии обозначены зеленым. Цветное изображение представляет из себя объемную минералогическую модель с относительным содержанием минеральных компонентов
Объемный прогноз зон вероятного развития коллектора результатов инверсии был выполнен с использованием алгоритма Random Forest, где в качестве признаков модели применены инверсионные параметры Ламе.
На рисунке 4 показан разрез прогнозного куба, отражающий вероятностное распределение коллектора в пределах карбонатов эйфельского яруса. Также на рисунке 4 показан в качестве примера разрез одного из восстановленных в результате синхронной инверсии упругих параметров —
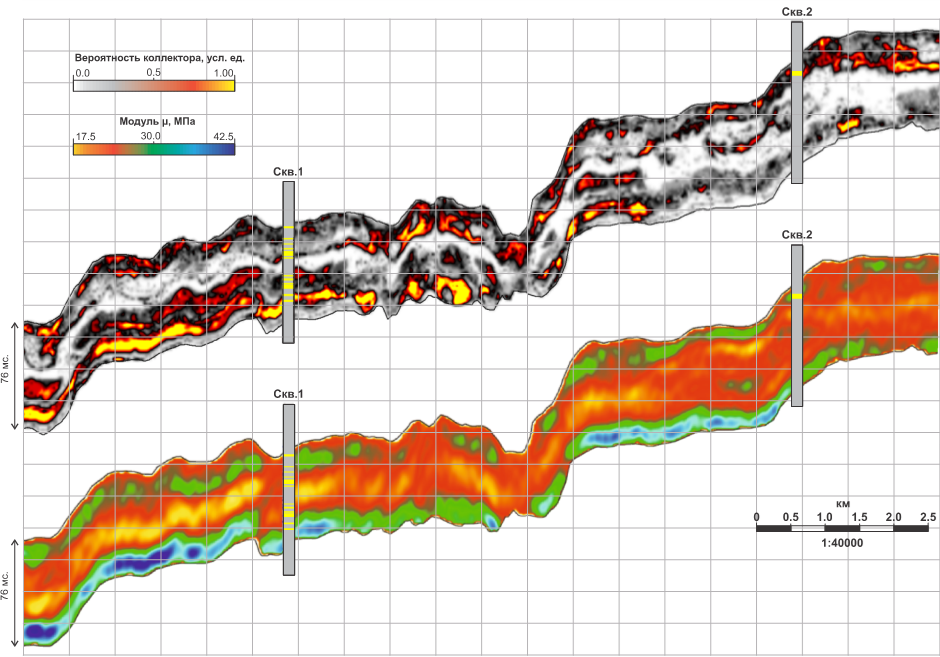
Рисунок 4. Интервал эйфельских карбонатов (бийско-афонинская толща). На верхнем разрезе показан прогноз распространения коллектора по результатам LMR-инверсии. Нижний разрез представляет разрез модуля
Совместный анализ восстановленных параметров Ламе и результата прогноза распространения коллектора, полученного с помощью алгоритма машинного обучения, показывает, что использование
Выводы
Проведенные исследования показали высокую информативность LMR сейсмической инверсии при анализе карбонатных разрезов. Для данных Оренбургской области результаты такой инверсии продемонстрировали высокую согласованность с данными ГИС: коэффициенты корреляции между восстановленными модулями
Совместное использование инверсии в параметризации Грея и алгоритма Random Forest способствовало выделению зон с повышенной вероятностью развития коллектора.
Таким образом, LMR-инверсия может рассматриваться как перспективный инструмент анализа слабоконтрастных карбонатных разрезов, расширяющий возможности существующих подходов к интерпретации сейсмических данных.
Благодарности
Авторы выражают глубокую признательность д. ф.-м. н. Г. М. Митрофанову, к. ф.-м. н. А. А. Дучкову за координацию исследований. Отдельная благодарность коллективу разработки программного модуля VersaBox за предоставленный доступ к инструментам динамической интерпретации, а также коллективу «Газпромнефть НТЦ» за плодотворное сотрудничество. Работа была выполнена при финансовой поддержке Министерства науки и высшего образования Российской Федерации (проект № FSUS-2025-0015).
1. Fagereva V. A. Expanding the possibilities of synchronous inversion in carbonates using a sedimentological concept // PROneft. Professionally about Oil. — 2023. — Vol. 8. — № 4. — Pp. 115–120. — https://doi.org/10.51890/2587-7399-2023-8-4-115-120 (in Russ.).
2. Goodway B. Improved AVO fluid detection and lithology discrimination using Lamé petrophysical parameters / B. Goodway, T. Chen, J. Downton // 67th Annual International Meeting, SEG: Expanded Abstracts. — Dallas, 1997. — Pp. 183–186.
3. Gray F. D. Case histories. Inversion for rock properties / F. D. Gray, E. A. Andersen // 62nd EAGE Conference & Exhibition. — Glasgow, 2000.
4. Urosevic M. LMR. A robust reservoir properties indicator in carbonate reservoirs / M. Urosevic, S. Amiri Besheli, S. S. Hendi, J. Vali // 66th EAGE Conference & Exhibition. — Paris, 2004.
5. Reza M. F. Carbonate reservoir characterization using simultaneous inversion in field “X” / M. F. Reza, M. S. Rosid, M. W. Haidar // AIP Conference Proceedings. — 2019. — Vol. 2168. — https://doi.org/10.1063/1.5132450.
6. Voskresensky Yu. N. Study of amplitude variation in seismic reflections for hydrocarbon exploration and prospecting / Voskresensky Yu. N. — Moscow: Gubkin Russian State University of Oil and Gas, 2001 (in Russ.).
7. Aki K. Quantitative Seismology / Aki K., Richards P. G. — San Francisco: W. H. Freeman, 1980.
8. Oldenburg D. W. Recovery of the acoustic impedance from reflection seismograms / Oldenburg D. W., Scheuer T., Levy S. // Geophysics. — 1983. — Vol. 48. — № 10. — Pp. 1318–1337.
9. Korchuganov V. D. Simultaneous VersaBox: software package for amplitude simultaneous seismic inversion / Korchuganov V. D., Pobezhimov E. A. // Certificate of state registration of computer software № 2025611730. — 2024 (in Russ.).
10. Breiman L. Random forests / Breiman L. // Machine Learning. — 2001. — Vol. 45. — № 1. — Pp. 5–32.
11. Vilesov A. P. Upper Paleozoic reef systems of the Rubezhinsky Trough (southern part of the Buzuluk Depression) / Vilesov A. P., Ledenev V. S., Solodov D. V., Filichev A. V., Bogomolova N. V., Makarova L. I., Grebenkina N. J., Kazachkova A. G., Sidubaev A. S. // PROneft. Professionally about Oil. — 2021. — Vol. 6. — № 3. — Pp. 30–42. — https://doi.org/10.51890/2587-7399-2021-6-3-30-42 (in Russ.) (in Russ.).
12. Grebenkina N. Yu. The Vorobyevsky terrigenous complex of the western part of the Rubezhinsky trough: new data on structural features and petroleum potential / Grebenkina N. Yu., Ekimenko A. V., Vilesov A. P., Ledenev V. S., Sidubaev A. S. // Geosciences: Time of Change, Time of Opportunities. — Saint Petersburg, 2023. — Pp. 35–38 (in Russ.).
13. Bacon M. Seismic amplitude: an interpreter’s handbook. / Bacon M., Simm R. — Cambridge: Cambridge University Press, 2014.
14. Vilesov A. P. Genesis of dolomite reservoirs of biysk-afonian carbonate complex in Orenburg region / Vilesov A. P., Chertina K. N., Vorontsov I. P., Devyatka N. P. // Geology, geophysics and development of oil and gas fields. — 2014. — № 11. — Pp. 25–34 (in Russ.).







