Mexico, Mexico
Russian Federation
The Thomsen parameters epsilon, gamma and delta characterize seismic anisotropy of thin-layered rocks such as shales; this is the anisotropy of the VTI symmetry. Shales are a classic example of the VTI anisotropy. However, transversely isotropic VTI shales become orthorhombic (the ORT model) due to the stress-induced azimuthal anisotropy and/or vertical fractures in shale plays. The azimuthal anisotropy turns out to be stronger than the intrinsic VTI anisotropy of the thin-layered shales. Based on the analysis of the velocity data obtained in the ultrasonic experiment, we estimate the Thomsen parameters epsilon, gamma and delta in the synthetic rock samples of vertically fractured shales; there is physical modeling of the orthorhombic medium ORT. Note that, unlike the VTI medium, the ORT medium is identified by a pair of each of the Thomsen parameters, i.e., two epsilons, two gammas, and two deltas. In each such pair (e.g., delta_1, delta_2), one of the parameters (i.e., delta_1) is determined in the vertical yz plane (this is the plane of fractures), and the other (delta_2) is for the vertical xz plane. It turned out that delta_1 is equal to the delta parameter, which characterizes the intrinsic VTI anisotropy of the shales. This turned out to be true for both epsilon_1 and gamma_1. As for the second Thomsen parameter, which is defined in the xz plane (that is, "epsilon", "gamma" and "delta" with index "2"), we found that our mnemonic formula "ORT = VTI + HTI" is only suitable for the parameter delta_2, but not for epsilon_2 and gamma_2. Namely, the value of the parameter delta_2 is almost equal to the sum "delta_VTI + delta_HTI", that is the sum of the parameters "delta" in the VTI and the HTI, respectively. (Let us clarify that "HTI" is an "equivalent HTI medium". That is, there are exactly the same fractures in the equivalent HTI model as in the sought ORT model. The difference is that in the equivalent HTI model the fractures are embedded in an isotropic rock matrix, whereas in the ORT model this rock matrix is represented by the VTI-shale rock.) The mnemonic formula "ORT = VTI + HTI" turned out to be inaccurate for the other two Thomsen parameters epsilon_2 and gamma_2. Note that there are long analytical formulas for them, which we upgrade and instead derive shorter approximate formulas for epsilon_2 and gamma_2.
shales, anisotropy, fractures, VTI, HTI, orthorhombic medium, Thomsen parameters.
Введение
Сланцевые породы обладают ярко выраженной «полярной» анизотропией, описываемой трансверсально-изотропной моделью VTI (рис. 1), которая задается пятью параметрами Томсена: ε, γ, δ, VP0 и VS0 [1], из них особое внимание уделяется здесь параметру δ.
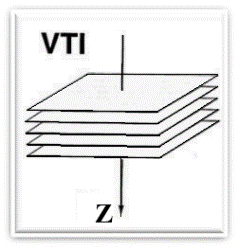
Рисунок 1. В модели VTI ось z — это вертикальная (Vertical) ось симметрии трансверсально-изотропной среды, и поэтому среда VTI так и называется, т. е. Vertical Transverse Isotropy
Параметр δ — это единственный параметр Томсена, который определяется по данным отраженных P-волн напрямую (в отличие от ε), например по азимутальному скоростному анализу NMO [2, 3]. А именно, в результате азимутального анализа скоростей NMO получается карта направления трещиноватости, как это показано на рисунке 2 [4]. Кроме направления трещиноватости, азимутальный анализ скорости NMO дает параметр Томсена δ, как это показано на рисунке 3 [5, 6, 7]. Параметр δ выражает относительную разницу между квадратами минимальной и максимальной скоростей NMO:
. (1)
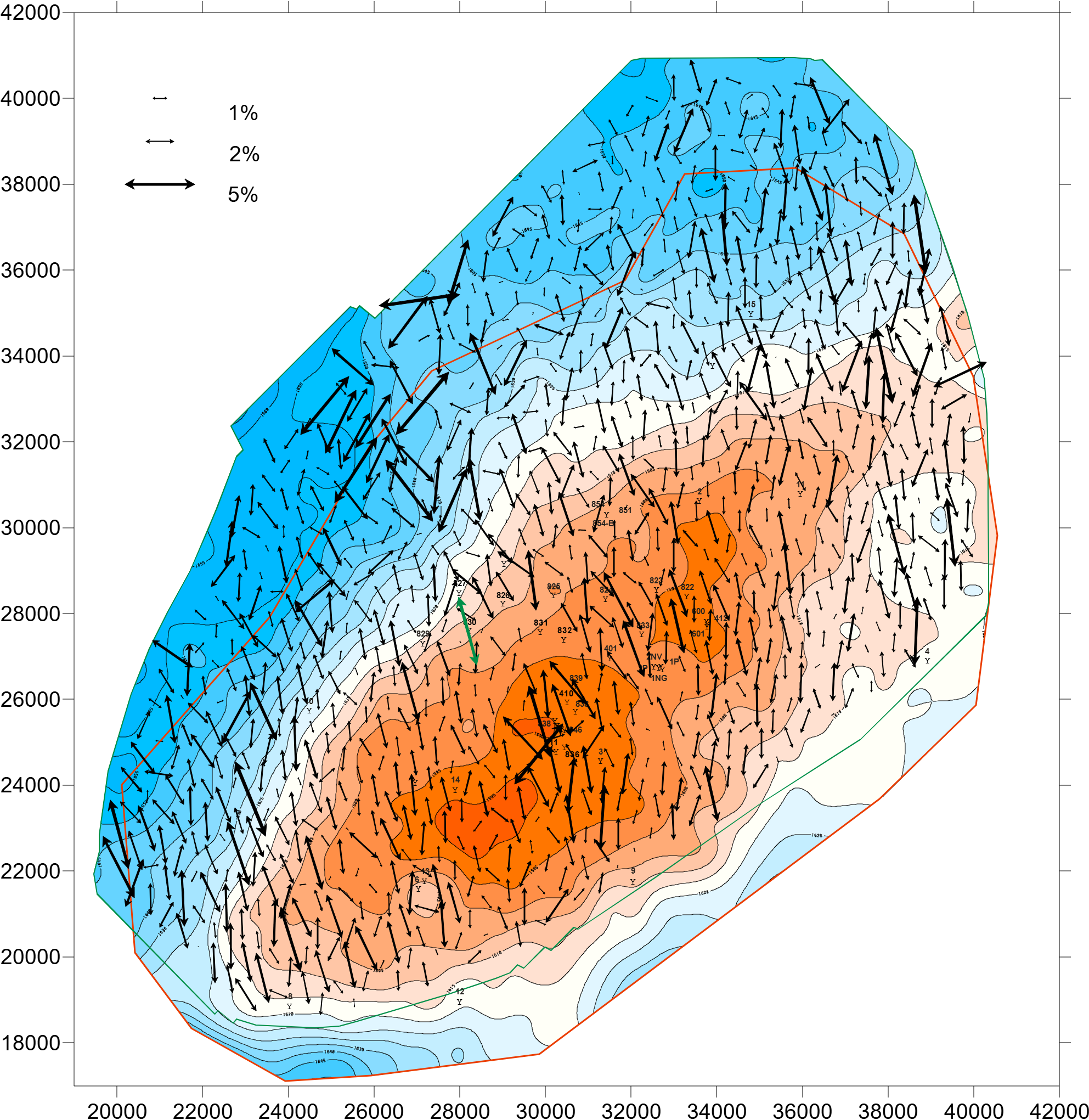
Рисунок 2. Распределение по площади направлений бόльшей полуоси NMO-эллипса эффективной скорости, вычисленной по горизонтам суходудинской свиты (СД3). Размер стрелки соответствует величине параметра Томсена δ. Цветом показана структурная карта по горизонту СД3 (Пеляткинская площадь). (Рисунок из работы [4], с разрешения авторов.)
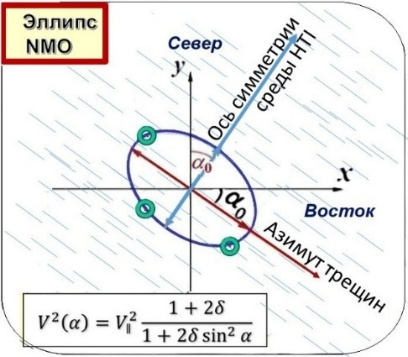
Рисунок 3. Эллипс NMO. Вид сверху, в горизонтальной плоскости xy. Бόльшая полуось эллипса ориентирована по азимуту трещин
Сначала рассмотрим собственную VTI-анизотропию сланцев (или же «полярную анизотропию»), которая характеризуется положительными параметрами Томсена ε и γ, т. е. они всегда больше нуля (
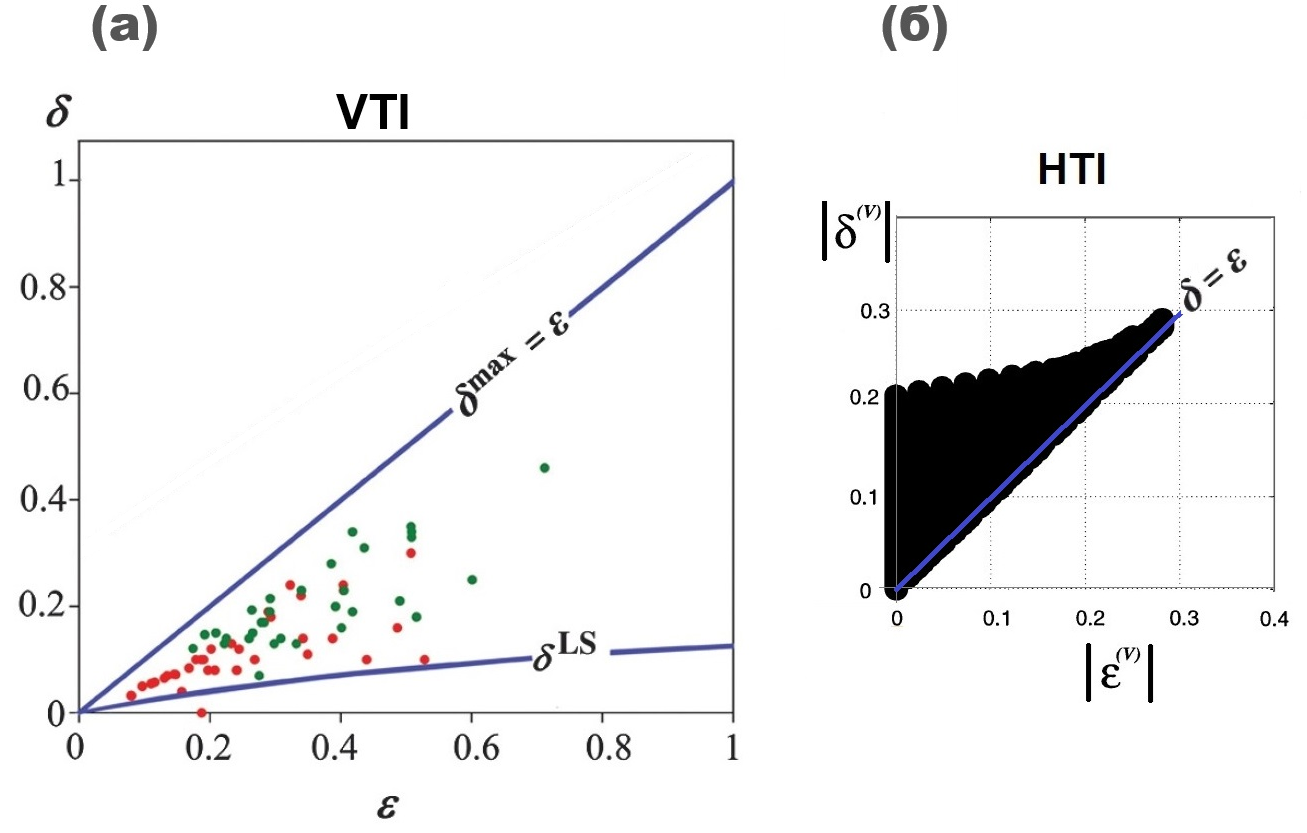
Рисунок 4. а) Параметры анизотропии (ε, δ) по реальным данным измерений скоростей на образцах сланцев: данные из работы Vernik [9] (показаны точками). Линиями обозначены теоретические границы области допустимых значений параметра δ, верхняя δmax и нижняя δLS. Верхняя граница определяется равенством δmax = ε. Нижняя граница определяется как δmin = δLS , где δLS — это параметр δ в модели Linear Slip (LS) [8]. б) Область допустимых значений для δ (как функции от ε) в HTI-модели трещиноватой среды. (Оригинальный рисунок взят из работы Bakulin [10] и переделан на абсолютные величины
В рамках модели VTI параметр δ может быть и отрицательным, например для водонасыщенных сланцев [11, 12]. Авторы статьи [13] обратили внимание на отрицательные значения δ для композита «вода — глина» (глина со связанной водой); отрицательные значения δ в глинистых сланцах, богатых смектитом, объясняются сильной способностью смектита связывать воду.
В настоящем исследовании мы покажем, что на величину параметра δ в сланцах может повлиять азимутальная анизотропия HTI из-за вертикальной трещиноватости и/или напряженного состояния геологической среды, как это показано на рисунке 5. В результате среда становится орторомбической [16]. И эта азимутальная анизотропия может радикально изменить величину параметров Томсена в сланцах (ε, γ, δ) и даже обратить их знак с плюса на минус. Простейшая анизотропная модель HTI описывает азимутально-анизотропную среду с параллельными вертикальными трещинами, «внедренными» в изотропную породу-матрицу, как это показано на рисунке 5. В противоположность параметру Томсена δ в модели VTI, в модели HTI параметр δ отрицательный, как и два других параметра анизотропии, ε и γ. Заметим, что для HTI-среды введено специальное обозначение для параметров анизотропии:
Итак, под действием горизонтальных напряжений (и/или вертикальной трещиноватости) возникает азимутальная анизотропия типа HTI (рис. 5). Однако из-за собственной VTI-анизотропии сланцев мы будем уже иметь дело не с HTI-моделью, а с орторомбической (ORT) [16, 18], как это показано на рисунке 6.
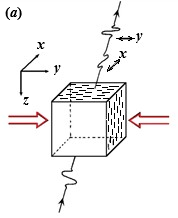
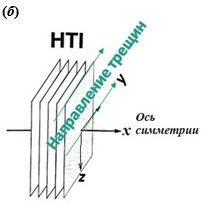
Рисунок 5. а) Модель HTI. Под действием горизонтальных напряжений (которые обозначены красными стрелками) возникает азимутальная анизотропия, которую также можно обнаружить и по расщеплению поперечных волн, S1 и S2. (Первоначально рисунок взят из Крэмпина [14] и немного модифицирован Кашубиным и нами [15].) б) В модели HTI ось x — это ось симметрии среды HTI; направление трещин — по оси y; плоскость yz — это плоскость трещин. Плоскость xz называется плоскостью оси симметрии
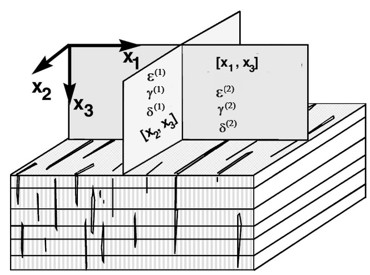
Рисунок 6. Орторомбическая модель (ORT) для вертикально-трещиноватых сланцев. Параметры Томсена ε, γ и δ с индексом (1) (т. е.
Эта модель ORT может быть представлена как суперпозиция двух, VTI и HTI (т. е. ORT = VTI + HTI). В орторомбической модели 9 независимых параметров анизотропии, а именно: два эпсилона (
Рассмотрим смысл формулы сложения ORT = VTI + HTI в применении ее к параметру Томсена
, (2)
причем
Орторомбическая модель
Мы изучаем анизотропию вертикально-трещиноватых сланцев, используя данные физического моделирования орторомбической модели [19]. Мы применяем математическую модель «линейного проскальзывания» (Linear Slip model) для орторомбической среды [16], которую мы коротко называем моделью ORT. В модели ORT имеется только 8 независимых параметров: 5 компонент
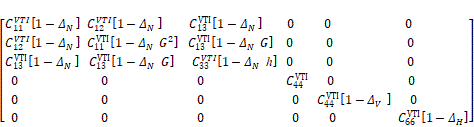 . (3)
. (3)
В уравнении (3) введены следующие сокращенные обозначения: и .
В эксперименте было пять образцов породы (с искусственными трещинами) орторомбической системы симметрии, отличающихся друг от друга концентрацией трещин [19, 21]. Вертикальные прямоугольные трещины квадратной формы были встроены в тонкослоистую породу-матрицу (последняя послужила нам как VTI-модель сланцевой породы), см. фотографию искусственных образцов трещиноватой породы на рисунке 7. Кроме этих пяти орторомбических образцов, был шестой, эталонный образец (модель VTI), выполненный из того же тонкослоистого материала; этот искусственный тонкослоистый образец VTI имитирует сланцеватую породу. Скорости P- и S-волн измерялись при углах падения 0° и 90°, и таким образом мы получили параметры Томсена ε и γ в плоскостях (xz) и (yz) соответственно:
; ; (4)
; . (5)

Рисунок 7. Физическое моделирование орторомбической модели для вертикально-трещиноватых сланцев. Пять образцов породы Ortho-i (i = 1, 2, …, 5) с искусственными вертикальными трещинами в тонкослоистом фундаменте. Дополнительно для сравнения использовался эталонный тонкослоистый образец REF, без трещин, имитирующий сланцевую породу-фундамент VTI. (Рисунок — из работы [19], с разрешения авторов.)
Для оценки параметра Томсена δ в орторомбической породе (а вернее — всех трех δ-параметров
В этом исследовании мы покажем, что величина параметров Томсена (т. е. ε, γ, δ) в вертикально трещиноватых сланцах сильно зависит от азимутальной анизотропии, возникающей из-за напряженного состояния земной коры и/или из-за наличия параллельных вертикальных трещин, в результате чего сланцы становятся орторомбическими. Эта азимутальная анизотропия может радикально изменить величину параметров Томсена и даже изменить их знак с положительного на отрицательный. Орторомбическая модель трещиноватых сланцев (ORT) может быть представлена как суперпозиция двух трансверсально-изотропных моделей, VTI и HTI; по принципу ORT = VTI + HTI (например, [21]). В модели ORT параллельные вертикальные трещины вызывают азимутальную анизотропию; этот эффект описывается «эквивалентной» моделью HTI [10, 18]. Однако помимо этой «наведенной» азимутальной анизотропии HTI, в рассматриваемой модели ORT также учитывается влияние собственной полярной анизотропии сланцев VTI, за счет их тонкослоистой микроструктуры [16].
В нашем физическом моделировании [19] измерялись скорости продольных волн (P) и двух поперечных (SV и SH) только на вертикальном и горизонтальном направлениях. Однако чтобы найти
. (6)
Аналогично формула для параметра
. (7)
Несмотря на отсутствие измерений скоростей на «косых» лучах (например,
, , . (8)
Поперечные ослабленности
 |
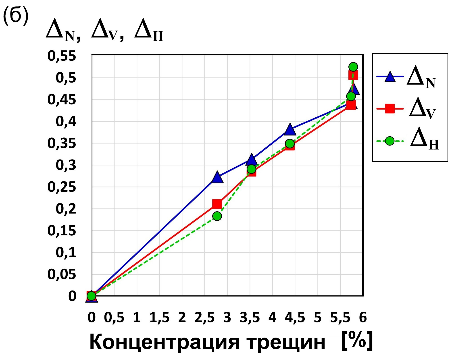 |
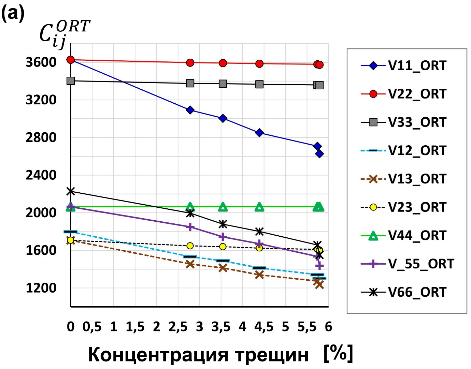
Рисунок 8. а) Нормированные компоненты тензора упругости {
Таблица 1. Компоненты тензора упругости {
|
Конц. трещин, % |
V11_ORT |
V22_ORT |
V33_ORT |
V44_ORT |
V_55_ORT |
V66_ORT |
V13_ORT |
V12_ORT |
V23_ORT |
|
0 (VTI) |
3626,7 |
3626,7 |
3402 |
2065,4 |
2065,4 |
2227,3 |
1706,924603 |
1797,560099 |
1706,924603 |
|
2,78 |
3091,603 |
3596,664163 |
3375,974265 |
2065,4 |
1851,144404 |
1996,249604 |
1455,078507 |
1532,341301 |
1648,623384 |
|
3,54 |
3004,744 |
3592,218769 |
3372,123793 |
2065,4 |
1743,402624 |
1880,062295 |
1414,197882 |
1489,289967 |
1639,860688 |
|
4,39 |
2850,265 |
3584,612855 |
3365,536625 |
2065,4 |
1669,892929 |
1800,790414 |
1341,491563 |
1412,723036 |
1624,783856 |
|
5,74 |
2707,08 |
3577,90805 |
3359,730771 |
2065,4 |
1536,103105 |
1656,51324 |
1274,100823 |
1341,753934 |
1611,403112 |
|
5,79 |
2627,141 |
3574,309926 |
3356,615416 |
2065,4 |
1438,750871 |
1551,52988 |
1236,47713 |
1302,132472 |
1604,186754 |
Таблица 2. Ослабленности трещин
|
Модель |
Конц. трещин, % |
Δ N | Δ V | Δ H |
Δ T = ( Δ V + Δ H )/2 |
|
VTI |
0 |
0 |
0 |
0 |
0 |
|
Ort-1 |
2,78 |
0,27331838 |
0,21053153 |
0,18288887 |
0,1967102 |
|
Ort-2 |
3,54 |
0,31357722 |
0,28430727 |
0,29068559 |
0,28749643 |
|
Ort-3 |
4,39 |
0,38234322 |
0,34403647 |
0,34859237 |
0,34631442 |
|
Ort-4 |
5,74 |
0,4428413 |
0,43688252 |
0,4568443 |
0,44686341 |
|
Ort-5 |
5,79 |
0,47526081 |
0,50536626 |
0,52413975 |
0,51475301 |
Заметим, что для эталонного образца VTI (сланец без вертикальных трещин) мы тоже восстановили тензор упругости {}, включая его недостающую недиагональную компоненту (что показано на рисунке 8а и в таблице 1 при нулевой концентрации трещин; для этого мы использовали формулы для в органических глинистых сланцах (organic mudrocks [8]).
Параметры Томсена ε и γ в орторомбической среде. Формула сложения ORT = VTI + HTI
Можно образно представить себе, что наша модель ORT для вертикально-трещиноватых сланцев построена по принципу ORT = VTI + HTI, где HTI означает «эквивалентная модель HTI» для трещиноватой среды, а VTI — это трансверсально-изотропная модель (с вертикальной осью симметрии) для тонкослоистой породы, такой как сланцы, представляющей фундамент породы ORT [18]. Простыми словами принцип сложения состоит в том, что порода ОRT представлена как совокупность двух элементов: трансверсально-изотропной породы-фундамента (модель VTI) и системы трещин (HTI). Вопрос состоит в том, можно ли использовать эту мнемоническую формулу сложения ORT = VTI + HTI для вычисления параметров Томсена в орторомбической среде, то есть
, . (9)
Бакулин с соавторами [18] предлагают использовать эти формулы сложения (9), которые в их обозначениях имеют следующий вид:
, , (10)
где
Таким образом, параметры Томсена
, . (11)
Компоненты VTI-тензора упругости {} даны в таблице 1 и на рисунке 8 при нулевой концентрации трещин. Полученные параметры Томсена
, . (12)
 |
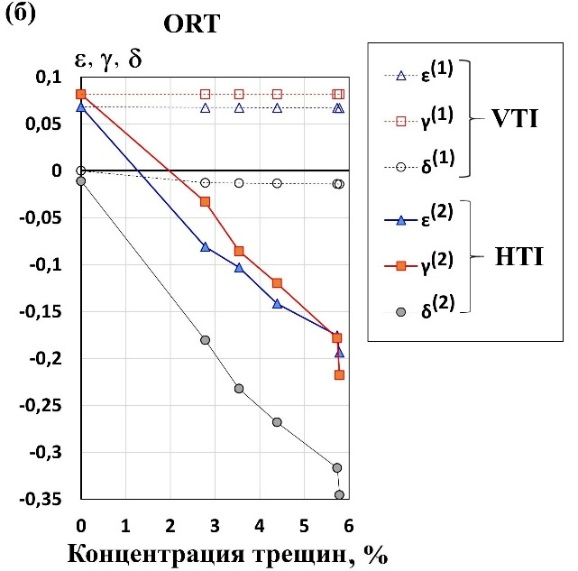 |
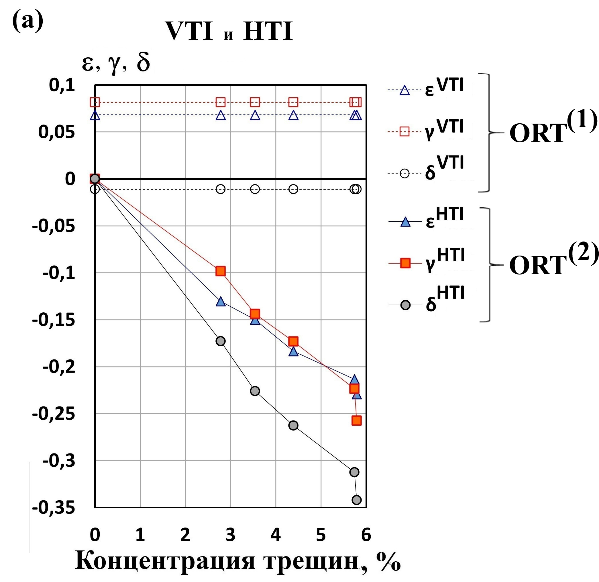
Рисунок 9. a) Параметры Томсена ε, γ и δ для «эквивалентной» трещиноватой породы HTI
Эквивалентная среда HTI. Параметры Томсена
; , (13)
где {
В эквивалентной HTI-модели Linear Slip [23], которую мы здесь используем, пятая компонента
, (14)
где и , .
Таблица 3. Нормированные компоненты тензора упругости
|
Конц. трещин, % |
C11_HTI |
C22_HTI |
C33_HTI |
C44_HTI |
C55_HTI |
C66_HTI |
C13_HTI |
C12_HTI |
C23_HTI |
|
0 (ISO) |
3641,403191 |
3641,403191 |
3641,403191 |
2227,3 |
2227,3 |
2227,3 |
1827,04313 |
1827,04313 |
1827,04313 |
|
2,78 |
3104,136827 |
3609,727891 |
3609,727891 |
2227,3 |
1996,249604 |
1996,249604 |
1557,47429 |
1557,47429 |
1763,06689 |
|
3,54 |
3016,925687 |
3605,038714 |
3605,038714 |
2227,3 |
1880,062295 |
1880,062295 |
1513,71685 |
1513,71685 |
1753,44619 |
|
4,39 |
2861,820406 |
3597,015007 |
3597,015007 |
2227,3 |
1800,790414 |
1800,790414 |
1435,89409 |
1435,89409 |
1736,88985 |
|
5,74 |
2718,054912 |
3589,941182 |
3589,941182 |
2227,3 |
1656,51324 |
1656,51324 |
1363,76097 |
1363,76097 |
1722,19252 |
|
5,79 |
2637,791828 |
3586,144743 |
3586,144743 |
2227,3 |
1551,52988 |
1551,52988 |
1323,48965 |
1323,48965 |
1714,26472 |
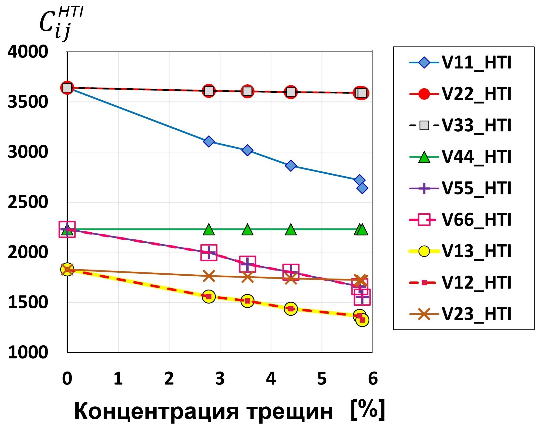
Рисунок 10. Компоненты тензора упругости {
Истинные (или же точные) параметры Томсена в орторомбической среде. Как оказалось, аппроксимация для
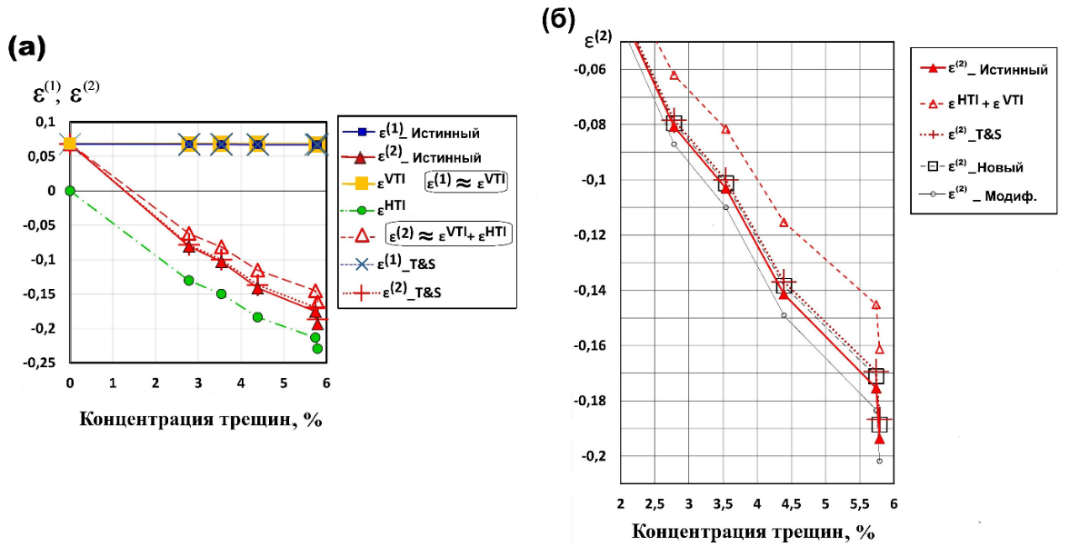
Рисунок 11. а) Параметры Томсена
Поскольку полученные аналитические формулы для истинных
Приближённые формулы для
Воспользуемся формулой Томсена — Сайерса [20] для
, (15)
где . На рисунке 11 показан результат расчета ε(2) по этой приближённой формуле (15); оказалось, что среднее отклонение от истинного
. (16)
Эта улучшенная и более компактная формула дает среднюю ошибку в определении
Предположим, что формулу для
, (17)
где , (18)
и где
; (19)
она дает довольно хорошую точность (график с пометкой «Модиф.» на рисунке 11) с относительной погрешностью 5,8 %; но эта погрешность все же больше, чем у формулы (16) («Новый» на рисунке 11).
Приближённые формулы для
Рассмотрим следующую приближённую формулу для
, (20)
где
, (21)
которую предложили авторы статьи [18] и которая в их обозначениях имеет вид:
Предполагая, что первый член
. (22)
Как показано на рисунке 11, графики
Параметры Томсена
По определению (уравнение (5)) выведем аналогичные формулы для параметров Томсена
; ; . (23)
Начнем с параметра Томсена
. (24)
Учитывая, что
. (25)
Затем, домножив числитель и знаменатель дроби на (
. (26)
Для
. (27)
По данным физического моделирования получается, что две поперечные ослабленности
; (28)
. (29)
Заметим, что обе эти формулы для
Интересно, что для
; ; (30)
; . (31)
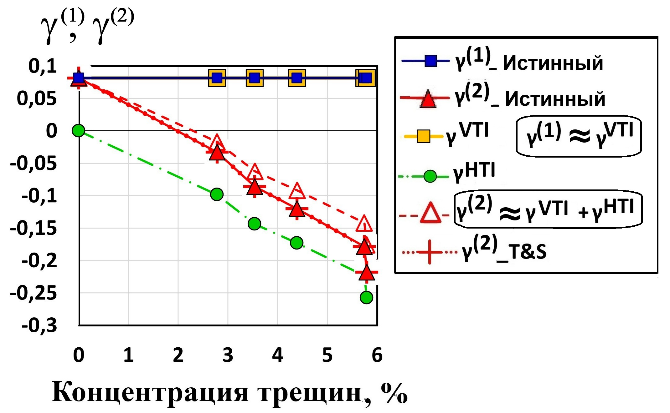
Рисунок 12. Параметры Томсена
Формула сложения VTI + HTI для
Формулу сложения
, (32)
где
Если пренебречь членом
Однако эта формула дает расхождение в 23 % с истинным
δ(
Параметр Томсена
, (35)
, (36)
. (37)
В таблицах 1 и 2 приведены компоненты тензоров ORT, VTI и HTI, т. е. {},
, (38)
получаем его истинное значение «
. (39)
Как это видно на рисунке 13б, эта формула Томсена — Сайерса плохо работает (т. е. средняя относительная разница с истинным
Таким образом, без каких-либо сложных предварительных вычислений орторомбического тензора упругости {
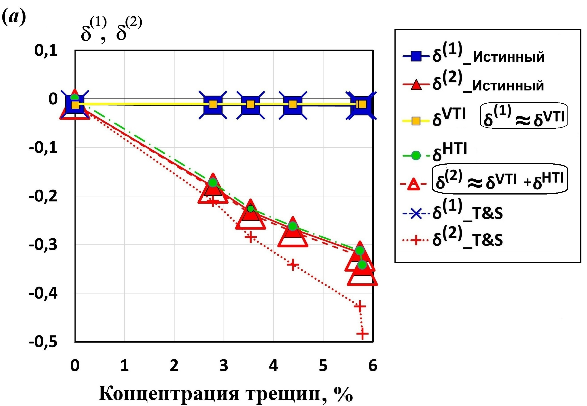 |
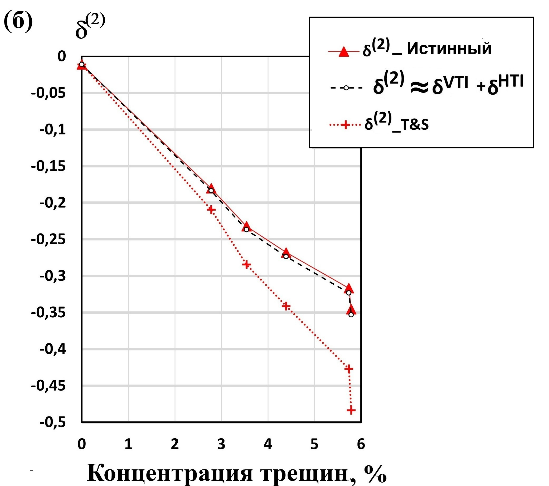 |
Рисунок 13. a) Параметры Томсена
Интересно, что тенденция поведения
Параметр Томсена
. (40)
Как показано на рисунке 13, график «
. (41)
Рисунок 13 показывает, что эта формула
Выводы
Формула сложения ORT = VTI + HTI помогает нам напрямую (без сложных предварительных вычислений) предсказать знак и приблизительную величину искомого параметра Томсена в трещиноватых сланцах (т. е.
Итак, для ε и γ в орторомбической среде ORT имеют место следующие единообразные формулы:
; ;
; .
Что касается формулы сложения ORT = VTI + HTI для
; .
Благодарности
Мы благодарим Мексиканский институт нефти (Instituto Mexicano del Petroleo (IMP)) за поддержку, номер проекта G.72040.
1. Thomsen L. Weak elastic anisotropy / Thomsen L. // Geophysics. — 1986. — № 51. — Pp. 1954–1966. — https://doi.org/10.1190/1.1442051.
2. Grechka V., Tsvankin I. 3-D description of normal moveout in anisotropic inhomogeneous media / Grechka V., Tsvankin I. // Geophysics. — 1998. — № 63. — Pp. 1079–1092. — https://doi.org/10.1190/1.1444386.
3. Chichinina T. Seismic Anisotropy Parameter δ for Fractured Reservoir Characterization Including Gas Saturation / Chichinina T., Mankenov O., Bezkhodarnov V., Avila-Carrera R. // In: Lin, J. (eds). Proceedings of the International Field Exploration and Development Conference 2024. IFEDC 2024. Springer Series in Geomechanics and Geoengineering (SSGG). — Springer, Singapore. — 2025. — Pp. 129–137. —https://doi.org/10.1007/978-981-96-2363-1_10.
4. Gorshkalev S. B. Rezul'taty izucheniya azimutal'noy anizotropii geologicheskogo razreza na Pelyatkinskoy ploschadi po dannym mnogovolnovogo VSP i seysmorazvedki 3D [Results of studying the azimuthal anisotropy of the subsurface at Pelyatkinsky area from multiwave VSP and seismic 3D data] / Gorshkalev S. B., Karsten V. V., Afonina E. V., Bekeshko P. S., Korsunov I. V. // Tehnologii seysmorazvedki. — 2011. — № 3. — C. 60–70 (in Russ.). EDN: https://elibrary.ru/OKCMGP
5. Chichinina T. I. Anizotropnaya model' ORT dlya gazonasyschennyh treschinovatyh porod [Anisotropic model "ORT" for gas-saturated fractured rocks] / Chichinina T. I., Detkov V. A., Mankenov O. K. // Sbornik materialov konferencii. «Tyumen' — 2024. Aktual'nye trendy nauchno-tehnologicheskogo razvitiya neftegazovoy otrasli». — Tyumen'. — 2024. — Pp. 24–27 (in Russ.).
6. Chichinina T. I. Parametr anizotropii δ kak indikator gazonasyschennosti treschinovatyh kollektorov [Anisotropy parameter δ as an indicator of gas saturation of fractured reservoirs] / Chichinina T. I., Bezhodarnov V. V., Mankenov O. K. // Conference Proceedings “Geomodel — 2024. 26-ya yubileynaya nauchno-prakticheskaya konferentsiya po voprosam geologorazvedki i razrabotki mestorozhdeniy nefti i gaza”, Russia, Gelendzhik, September 9–12, 2024. — Pp.114–118 (in Russ.). EDN: https://elibrary.ru/RAGLEA
7. Chichinina T. I. Anizotropiya slancev: ortorombicheskaya model' [Shale anisotropy: an orthorhombic model] / Chichinina T. I., Avila-Karrera R., Martyushev D. A. // Conference Proceedings "Nauka o slancah '25. Novye dannye". Moscow, Russia, April 7–8, 2025 (in Russ.).
8. Chichinina T. Physical bounds on C13 and anisotropy parameter δ for organic mudrocks / Chichinina T., Vernik L. // Geophysics. — 2018. — № 83(5). — Pp. A75 — A79. — https://doi.org/10.1190/geo2018-0035.1 EDN: https://elibrary.ru/YJFFFJ
9. Vernik L. Seismic Petrophysics in Quantitative Interpretation / Vernik L. // Publisher: Society of Exploration Geophysicists (SEG). — 2016. — P. 226. —https://doi.org/10.1190/1.9781560803256.
10. Bakulin A. Estimation of fracture parameters from reflection seismic data —Part I: HTI model due to a single fracture set / Bakulin A., Grechka V., Tsvankin I. // Geophysics. — 2000. — № 65(6). — Pp. 1788–1802. — https://doi.org/10.1190/1.1444863. EDN: https://elibrary.ru/LGBHKJ
11. Vernik L. Velocity anisotropy in shales: a petrophysical study / Vernik L., Liu X. // Geophysics. — 1997. — № 62. — Pp. 521–532. — https://doi.org/10.1190/1.1444162.
12. Chesnokov E. M. Mathematical modelling of anisotropy of illite-rich shale / Chesnokov E. M., Tiwary D. K., Bayuk I. O., Sparkman M. A., Brown R. L. // Geophysical Journal International. — 2009. — № 178(3). — Pp. 1625–1648. — https://doi.org/10.1111/j.1365-246X.2009.04244.x. EDN: https://elibrary.ru/MWYUDD
13. Bayuk I. O. Elastic moduli of anisotropic clay / Bayuk I. O., Ammerman M., Chesnokov E. M. // Geophysics. — 2007. — № 72(5). — P. D107 — D117. —https://doi.org/10.1190/1.2757624. EDN: https://elibrary.ru/KGPBKS
14. Crampin S. A decade of shear-wave splitting in the Earth’s crust: what does it mean? what use can we make of it? and what should we do next? / Crampin S., Lovel J. H. // Geophysical Journal International. — 1991. — № 107. — P. 387–407. —https://doi.org/10.1111/j.1365-246X.1991.tb01401.x.
15. Kashubin S. N. Seysmicheskaya anizotropiya i eksperimenty po ee izucheniyu na Urale i Vostochno-Evropeyskoy platforme [Seismic anisotropy and experiments on the anisotropy study in the Urals and the East European platform] / Kashubin S. N. — Ekaterinburg: UrO RAN, 2001 (in Russ.). EDN: https://elibrary.ru/WXCBLP
16. Schoenberg M. Orthorhombic media: modeling elastic wave behavior in a vertically fractured earth / Schoenberg M., Helbig K. // Geophysics. — 1997. — № 62. — P. 1954–1974. — https://doi.org/10.1190/1.1444297.
17. Schoenberg M. Elastic wave behavior across linear slip interfaces / Schoenberg M. // Journal of Acoustical Society of America. — 1980. № 68. — P. 1516–1521. — https://doi.org/10.1121/1.385077.
18. Bakulin A. Estimation of fracture parameters from reflection seismic data — Part II: Fractured models with orthorhombic symmetry / Bakulin A., Grechka V., Tsvankin I. // Geophysics. — 2000. — № 65(6). — P. 1803–1817. — https://doi.org/10.1190/1.1444864. EDN: https://elibrary.ru/LGCHML
19. Silva C. Experimental characterization of synthetic porous orthorhombic fractured medium: A physical modeling approach / Silva C., de Figueiredo J. J. S., Chichinina T., Nascimento M. J., Kirchhof L. // Ultrasonics. — 2019. — № 94. — P. 82–91. — https://doi.org/10.1016/j.ultras.2018.11.015.
20. Thomsen L., Sayers C. Anisotropy parameters for fractured shales / Thomsen L., Sayers C. // Second International Meeting for Applied Geoscience & Energy. Society of Exploration Geophysicists (SEG) and the American Association of Petroleum Geologists (AAPG). — 2022. — P. 150–154. DOI: https://doi.org/10.1190/image2022-3748535.1
21. Chichinina T. Anisotropy Models and Parameters of Fractured Rocks by Physical Modeling Data / Chichinina T., De Figueiredo J. J. S., Bulgakov I., Avila-Carrera R. // In: J. Lin (Ed.). Proceedings of the International Field Exploration and Development Conference 2023. Springer Series in Geomechanics and Geoengineering (SSGG). — Springer Nature. — 2024. — P. 1027–1036. — https://doi.org/10.1007/978-981-97-0468-2_81.
22. Chichinina T. Physical constraints on C13 for transversely isotropic shales and their applications / Chichinina T. // Geophysics. — 2017. — № 82(4). — P. WA105 — WA118. — https://doi.org/10.1190/geo2016-0656.1. EDN: https://elibrary.ru/YGIWIU
23. Schoenberg M. Seismic anisotropy of fractured rock / Schoenberg M., Sayers C. M. // Geophysics. — 1995. — № 60. — P. 204–211. — https://doi.org/10.1190/1.1443748.








