Мехико, Мексика
Россия
Параметры Томсена epsilon, gamma и delta характеризуют анизотропию упругих свойств тонкослоистой горной породы, такой как сланцы (т. е. симметрия VTI). Сланцы являются классическим примером анизотропии VTI. Однако трансверсально-изотропные VTI-сланцы становятся орторомбическими (модель ORT) из-за наведенной азимутальной анизотропии вследствие напряженного состояния геологической среды и/или вертикальной трещиноватости. И эта азимутальная анизотропия оказывается сильнее, чем собственная VTI-анизотропия сланцевого (тонкослоистого) пласта. Исходя из анализа данных измерений скоростей в ультразвуковом эксперименте, мы определили параметры Томсена epsilon, gamma и delta в искусственных образцах вертикально-трещиноватых сланцев (физическое моделирование орторомбической среды ORT). Заметим, что, в отличие от VTI-сланцев, в орторомбической среде ORT имеется по паре каждого из параметров Томсена, т. е. два epsilon, два gamma и два delta. В каждой такой паре (например, delta_1 и delta_2) один из параметров (т. е. delta_1) определяется в вертикальной плоскости yz (это плоскость трещин), а другой (delta_2) — в вертикальной плоскости xz. Оказалось, что delta_1 равен параметру delta, который характеризует собственную VTI-анизотропию сланцев. Это оказалось верным и для epsilon_1 и gamma_1. Что касается второго параметра Томсена, который определяется в плоскости xz (т. е. epsilon, gamma и delta с индексом 2), то мы обнаружили, что наша мнемоническая формула ORT = VTI + HTI годится только для параметра delta_2, а для epsilon_2 и gamma_2 — не годится. А именно: величина параметра delta_2 практически равна сумме delta_VTI + delta_HTI, т. е. сумме параметров delta в средах VTI и HTI соответственно. (Поясним, что HTI — это «эквивалентная HTI-среда», т. е. такая, в которой точно такие же трещины, как в искомой модели ORT. Отличие состоит в том, что в модели HTI трещины внедрены в изотропный скелет породы, тогда как в модели ORT этот скелет представлен тонкослоистой сланцевой породой VTI.) Мнемоническая формула ORT = VTI + HTI оказалась неточной для остальных двух параметров Томсена epsilon_2 и gamma_2. Заметим, что для них имеются длинные аналитические формулы, которые мы перепроверили и вывели вместо них более короткие приближённые формулы для epsilon_2 и gamma_2.
сланцы, анизотропия, трещины, VTI, HTI, орторомбическая среда, параметры Томсена.
Введение
Сланцевые породы обладают ярко выраженной «полярной» анизотропией, описываемой трансверсально-изотропной моделью VTI (рис. 1), которая задается пятью параметрами Томсена: ε, γ, δ, VP0 и VS0 [1], из них особое внимание уделяется здесь параметру δ.
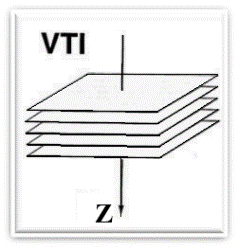
Рисунок 1. В модели VTI ось z — это вертикальная (Vertical) ось симметрии трансверсально-изотропной среды, и поэтому среда VTI так и называется, т. е. Vertical Transverse Isotropy
Параметр δ — это единственный параметр Томсена, который определяется по данным отраженных P-волн напрямую (в отличие от ε), например по азимутальному скоростному анализу NMO [2, 3]. А именно, в результате азимутального анализа скоростей NMO получается карта направления трещиноватости, как это показано на рисунке 2 [4]. Кроме направления трещиноватости, азимутальный анализ скорости NMO дает параметр Томсена δ, как это показано на рисунке 3 [5, 6, 7]. Параметр δ выражает относительную разницу между квадратами минимальной и максимальной скоростей NMO:
. (1)
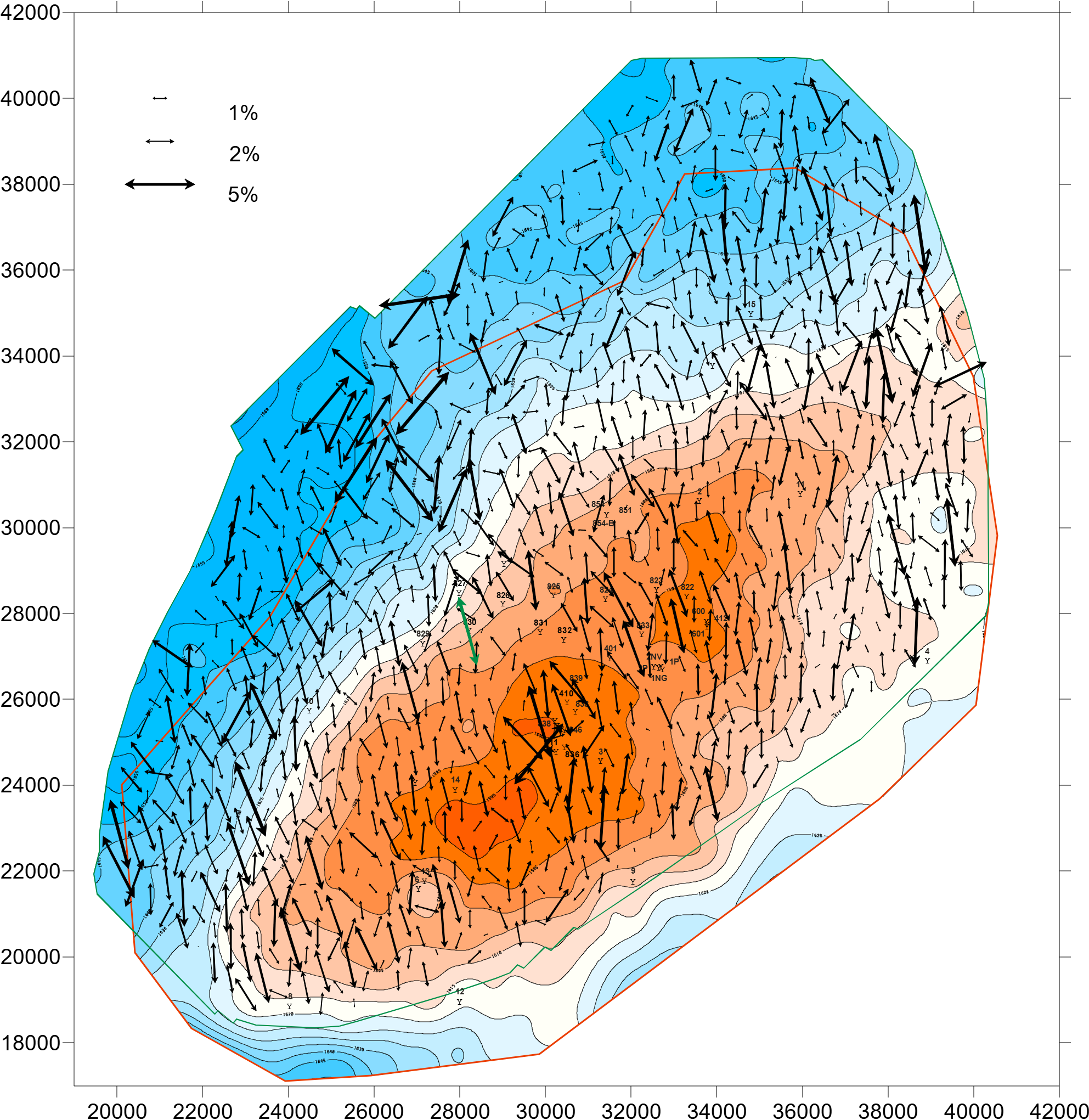
Рисунок 2. Распределение по площади направлений бόльшей полуоси NMO-эллипса эффективной скорости, вычисленной по горизонтам суходудинской свиты (СД3). Размер стрелки соответствует величине параметра Томсена δ. Цветом показана структурная карта по горизонту СД3 (Пеляткинская площадь). (Рисунок из работы [4], с разрешения авторов.)
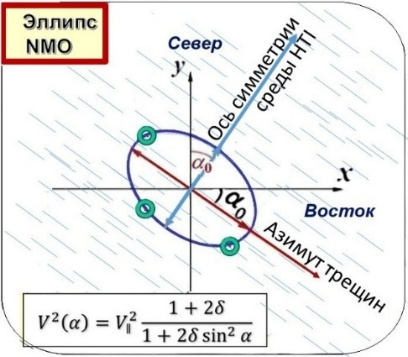
Рисунок 3. Эллипс NMO. Вид сверху, в горизонтальной плоскости xy. Бόльшая полуось эллипса ориентирована по азимуту трещин
Сначала рассмотрим собственную VTI-анизотропию сланцев (или же «полярную анизотропию»), которая характеризуется положительными параметрами Томсена ε и γ, т. е. они всегда больше нуля (
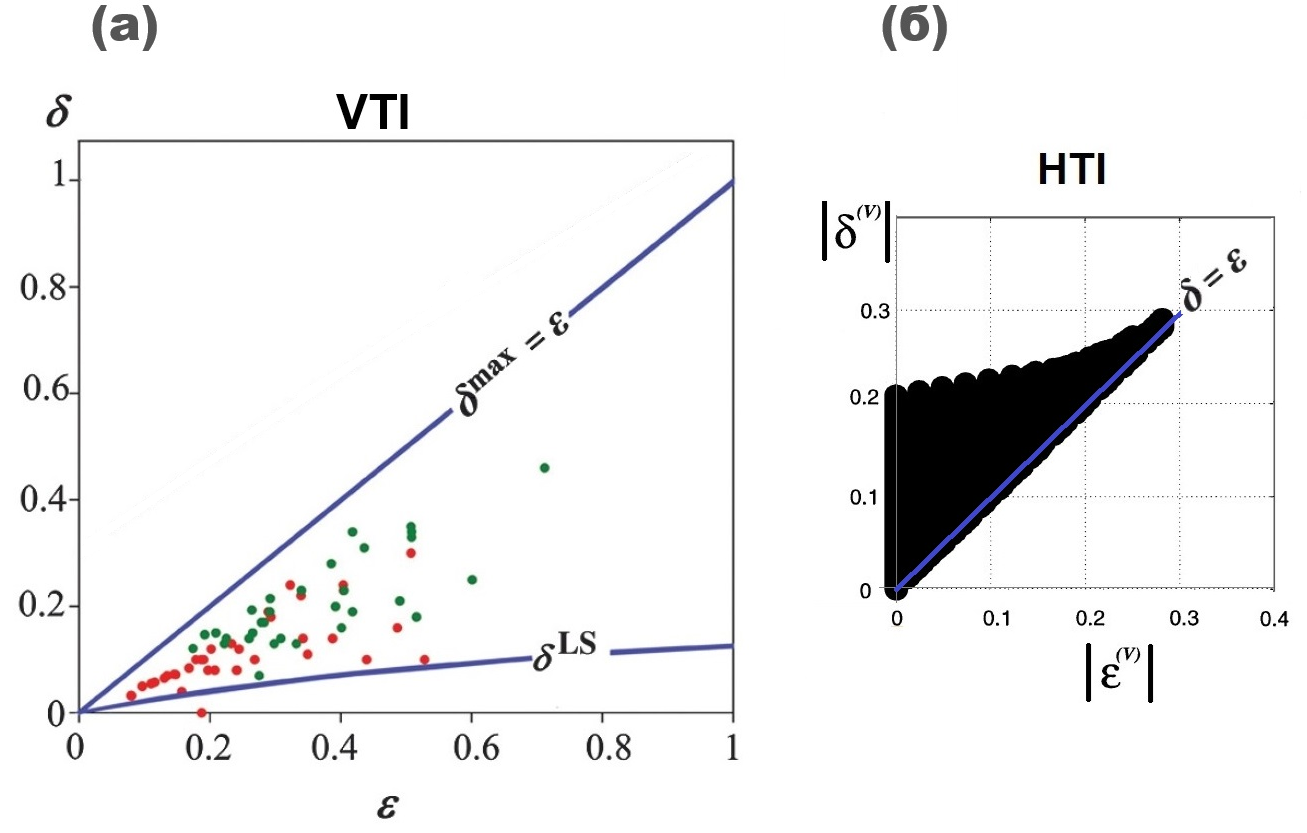
Рисунок 4. а) Параметры анизотропии (ε, δ) по реальным данным измерений скоростей на образцах сланцев: данные из работы Vernik [9] (показаны точками). Линиями обозначены теоретические границы области допустимых значений параметра δ, верхняя δmax и нижняя δLS. Верхняя граница определяется равенством δmax = ε. Нижняя граница определяется как δmin = δLS , где δLS — это параметр δ в модели Linear Slip (LS) [8]. б) Область допустимых значений для δ (как функции от ε) в HTI-модели трещиноватой среды. (Оригинальный рисунок взят из работы Bakulin [10] и переделан на абсолютные величины
В рамках модели VTI параметр δ может быть и отрицательным, например для водонасыщенных сланцев [11, 12]. Авторы статьи [13] обратили внимание на отрицательные значения δ для композита «вода — глина» (глина со связанной водой); отрицательные значения δ в глинистых сланцах, богатых смектитом, объясняются сильной способностью смектита связывать воду.
В настоящем исследовании мы покажем, что на величину параметра δ в сланцах может повлиять азимутальная анизотропия HTI из-за вертикальной трещиноватости и/или напряженного состояния геологической среды, как это показано на рисунке 5. В результате среда становится орторомбической [16]. И эта азимутальная анизотропия может радикально изменить величину параметров Томсена в сланцах (ε, γ, δ) и даже обратить их знак с плюса на минус. Простейшая анизотропная модель HTI описывает азимутально-анизотропную среду с параллельными вертикальными трещинами, «внедренными» в изотропную породу-матрицу, как это показано на рисунке 5. В противоположность параметру Томсена δ в модели VTI, в модели HTI параметр δ отрицательный, как и два других параметра анизотропии, ε и γ. Заметим, что для HTI-среды введено специальное обозначение для параметров анизотропии:
Итак, под действием горизонтальных напряжений (и/или вертикальной трещиноватости) возникает азимутальная анизотропия типа HTI (рис. 5). Однако из-за собственной VTI-анизотропии сланцев мы будем уже иметь дело не с HTI-моделью, а с орторомбической (ORT) [16, 18], как это показано на рисунке 6.
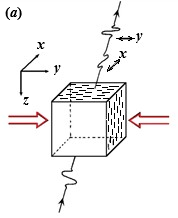
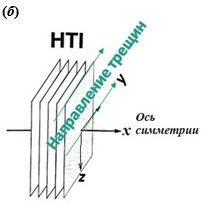
Рисунок 5. а) Модель HTI. Под действием горизонтальных напряжений (которые обозначены красными стрелками) возникает азимутальная анизотропия, которую также можно обнаружить и по расщеплению поперечных волн, S1 и S2. (Первоначально рисунок взят из Крэмпина [14] и немного модифицирован Кашубиным и нами [15].) б) В модели HTI ось x — это ось симметрии среды HTI; направление трещин — по оси y; плоскость yz — это плоскость трещин. Плоскость xz называется плоскостью оси симметрии
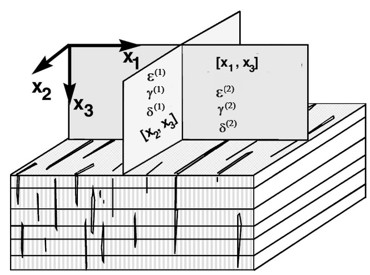
Рисунок 6. Орторомбическая модель (ORT) для вертикально-трещиноватых сланцев. Параметры Томсена ε, γ и δ с индексом (1) (т. е.
Эта модель ORT может быть представлена как суперпозиция двух, VTI и HTI (т. е. ORT = VTI + HTI). В орторомбической модели 9 независимых параметров анизотропии, а именно: два эпсилона (
Рассмотрим смысл формулы сложения ORT = VTI + HTI в применении ее к параметру Томсена
, (2)
причем
Орторомбическая модель
Мы изучаем анизотропию вертикально-трещиноватых сланцев, используя данные физического моделирования орторомбической модели [19]. Мы применяем математическую модель «линейного проскальзывания» (Linear Slip model) для орторомбической среды [16], которую мы коротко называем моделью ORT. В модели ORT имеется только 8 независимых параметров: 5 компонент
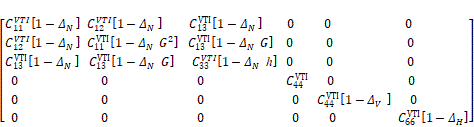 . (3)
. (3)
В уравнении (3) введены следующие сокращенные обозначения: и .
В эксперименте было пять образцов породы (с искусственными трещинами) орторомбической системы симметрии, отличающихся друг от друга концентрацией трещин [19, 21]. Вертикальные прямоугольные трещины квадратной формы были встроены в тонкослоистую породу-матрицу (последняя послужила нам как VTI-модель сланцевой породы), см. фотографию искусственных образцов трещиноватой породы на рисунке 7. Кроме этих пяти орторомбических образцов, был шестой, эталонный образец (модель VTI), выполненный из того же тонкослоистого материала; этот искусственный тонкослоистый образец VTI имитирует сланцеватую породу. Скорости P- и S-волн измерялись при углах падения 0° и 90°, и таким образом мы получили параметры Томсена ε и γ в плоскостях (xz) и (yz) соответственно:
; ; (4)
; . (5)

Рисунок 7. Физическое моделирование орторомбической модели для вертикально-трещиноватых сланцев. Пять образцов породы Ortho-i (i = 1, 2, …, 5) с искусственными вертикальными трещинами в тонкослоистом фундаменте. Дополнительно для сравнения использовался эталонный тонкослоистый образец REF, без трещин, имитирующий сланцевую породу-фундамент VTI. (Рисунок — из работы [19], с разрешения авторов.)
Для оценки параметра Томсена δ в орторомбической породе (а вернее — всех трех δ-параметров
В этом исследовании мы покажем, что величина параметров Томсена (т. е. ε, γ, δ) в вертикально трещиноватых сланцах сильно зависит от азимутальной анизотропии, возникающей из-за напряженного состояния земной коры и/или из-за наличия параллельных вертикальных трещин, в результате чего сланцы становятся орторомбическими. Эта азимутальная анизотропия может радикально изменить величину параметров Томсена и даже изменить их знак с положительного на отрицательный. Орторомбическая модель трещиноватых сланцев (ORT) может быть представлена как суперпозиция двух трансверсально-изотропных моделей, VTI и HTI; по принципу ORT = VTI + HTI (например, [21]). В модели ORT параллельные вертикальные трещины вызывают азимутальную анизотропию; этот эффект описывается «эквивалентной» моделью HTI [10, 18]. Однако помимо этой «наведенной» азимутальной анизотропии HTI, в рассматриваемой модели ORT также учитывается влияние собственной полярной анизотропии сланцев VTI, за счет их тонкослоистой микроструктуры [16].
В нашем физическом моделировании [19] измерялись скорости продольных волн (P) и двух поперечных (SV и SH) только на вертикальном и горизонтальном направлениях. Однако чтобы найти
. (6)
Аналогично формула для параметра
. (7)
Несмотря на отсутствие измерений скоростей на «косых» лучах (например,
, , . (8)
Поперечные ослабленности
 |
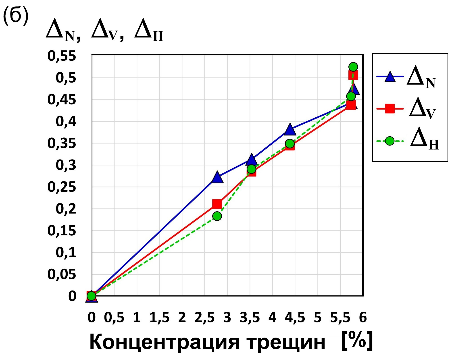 |
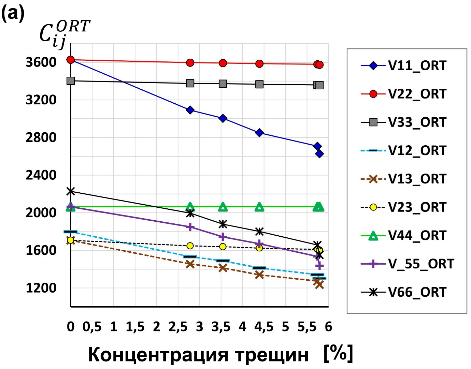
Рисунок 8. а) Нормированные компоненты тензора упругости {
Таблица 1. Компоненты тензора упругости {
|
Конц. трещин, % |
V11_ORT |
V22_ORT |
V33_ORT |
V44_ORT |
V_55_ORT |
V66_ORT |
V13_ORT |
V12_ORT |
V23_ORT |
|
0 (VTI) |
3626,7 |
3626,7 |
3402 |
2065,4 |
2065,4 |
2227,3 |
1706,924603 |
1797,560099 |
1706,924603 |
|
2,78 |
3091,603 |
3596,664163 |
3375,974265 |
2065,4 |
1851,144404 |
1996,249604 |
1455,078507 |
1532,341301 |
1648,623384 |
|
3,54 |
3004,744 |
3592,218769 |
3372,123793 |
2065,4 |
1743,402624 |
1880,062295 |
1414,197882 |
1489,289967 |
1639,860688 |
|
4,39 |
2850,265 |
3584,612855 |
3365,536625 |
2065,4 |
1669,892929 |
1800,790414 |
1341,491563 |
1412,723036 |
1624,783856 |
|
5,74 |
2707,08 |
3577,90805 |
3359,730771 |
2065,4 |
1536,103105 |
1656,51324 |
1274,100823 |
1341,753934 |
1611,403112 |
|
5,79 |
2627,141 |
3574,309926 |
3356,615416 |
2065,4 |
1438,750871 |
1551,52988 |
1236,47713 |
1302,132472 |
1604,186754 |
Таблица 2. Ослабленности трещин
|
Модель |
Конц. трещин, % |
Δ N | Δ V | Δ H |
Δ T = ( Δ V + Δ H )/2 |
|
VTI |
0 |
0 |
0 |
0 |
0 |
|
Ort-1 |
2,78 |
0,27331838 |
0,21053153 |
0,18288887 |
0,1967102 |
|
Ort-2 |
3,54 |
0,31357722 |
0,28430727 |
0,29068559 |
0,28749643 |
|
Ort-3 |
4,39 |
0,38234322 |
0,34403647 |
0,34859237 |
0,34631442 |
|
Ort-4 |
5,74 |
0,4428413 |
0,43688252 |
0,4568443 |
0,44686341 |
|
Ort-5 |
5,79 |
0,47526081 |
0,50536626 |
0,52413975 |
0,51475301 |
Заметим, что для эталонного образца VTI (сланец без вертикальных трещин) мы тоже восстановили тензор упругости {}, включая его недостающую недиагональную компоненту (что показано на рисунке 8а и в таблице 1 при нулевой концентрации трещин; для этого мы использовали формулы для в органических глинистых сланцах (organic mudrocks [8]).
Параметры Томсена ε и γ в орторомбической среде. Формула сложения ORT = VTI + HTI
Можно образно представить себе, что наша модель ORT для вертикально-трещиноватых сланцев построена по принципу ORT = VTI + HTI, где HTI означает «эквивалентная модель HTI» для трещиноватой среды, а VTI — это трансверсально-изотропная модель (с вертикальной осью симметрии) для тонкослоистой породы, такой как сланцы, представляющей фундамент породы ORT [18]. Простыми словами принцип сложения состоит в том, что порода ОRT представлена как совокупность двух элементов: трансверсально-изотропной породы-фундамента (модель VTI) и системы трещин (HTI). Вопрос состоит в том, можно ли использовать эту мнемоническую формулу сложения ORT = VTI + HTI для вычисления параметров Томсена в орторомбической среде, то есть
, . (9)
Бакулин с соавторами [18] предлагают использовать эти формулы сложения (9), которые в их обозначениях имеют следующий вид:
, , (10)
где
Таким образом, параметры Томсена
, . (11)
Компоненты VTI-тензора упругости {} даны в таблице 1 и на рисунке 8 при нулевой концентрации трещин. Полученные параметры Томсена
, . (12)
 |
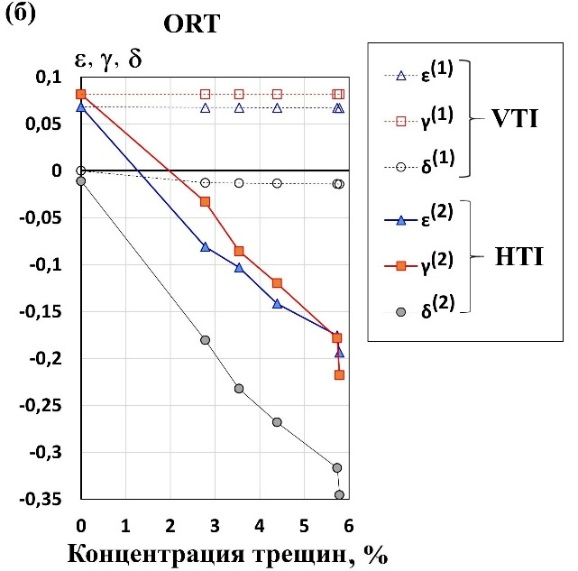 |
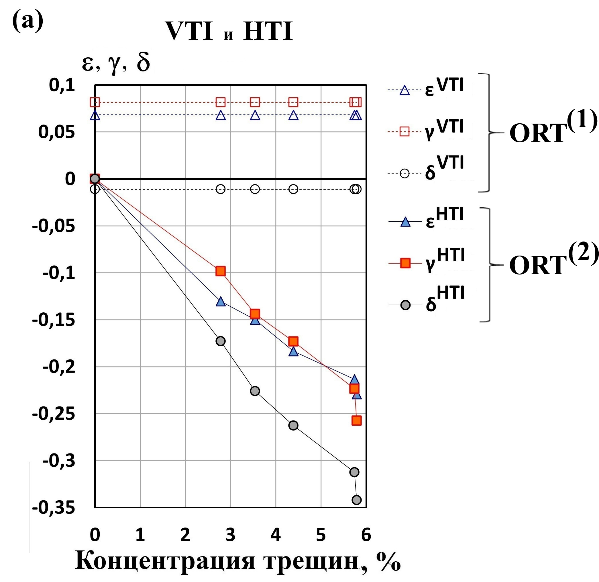
Рисунок 9. a) Параметры Томсена ε, γ и δ для «эквивалентной» трещиноватой породы HTI
Эквивалентная среда HTI. Параметры Томсена
; , (13)
где {
В эквивалентной HTI-модели Linear Slip [23], которую мы здесь используем, пятая компонента
, (14)
где и , .
Таблица 3. Нормированные компоненты тензора упругости
|
Конц. трещин, % |
C11_HTI |
C22_HTI |
C33_HTI |
C44_HTI |
C55_HTI |
C66_HTI |
C13_HTI |
C12_HTI |
C23_HTI |
|
0 (ISO) |
3641,403191 |
3641,403191 |
3641,403191 |
2227,3 |
2227,3 |
2227,3 |
1827,04313 |
1827,04313 |
1827,04313 |
|
2,78 |
3104,136827 |
3609,727891 |
3609,727891 |
2227,3 |
1996,249604 |
1996,249604 |
1557,47429 |
1557,47429 |
1763,06689 |
|
3,54 |
3016,925687 |
3605,038714 |
3605,038714 |
2227,3 |
1880,062295 |
1880,062295 |
1513,71685 |
1513,71685 |
1753,44619 |
|
4,39 |
2861,820406 |
3597,015007 |
3597,015007 |
2227,3 |
1800,790414 |
1800,790414 |
1435,89409 |
1435,89409 |
1736,88985 |
|
5,74 |
2718,054912 |
3589,941182 |
3589,941182 |
2227,3 |
1656,51324 |
1656,51324 |
1363,76097 |
1363,76097 |
1722,19252 |
|
5,79 |
2637,791828 |
3586,144743 |
3586,144743 |
2227,3 |
1551,52988 |
1551,52988 |
1323,48965 |
1323,48965 |
1714,26472 |
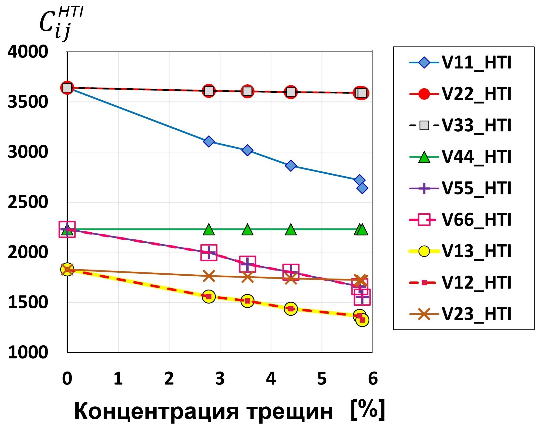
Рисунок 10. Компоненты тензора упругости {
Истинные (или же точные) параметры Томсена в орторомбической среде. Как оказалось, аппроксимация для
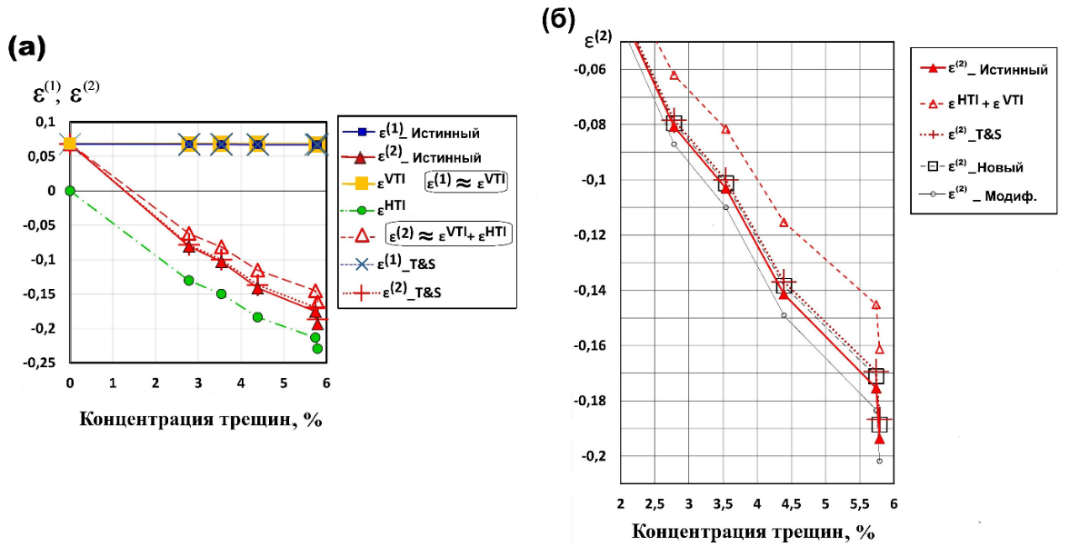
Рисунок 11. а) Параметры Томсена
Поскольку полученные аналитические формулы для истинных
Приближённые формулы для
Воспользуемся формулой Томсена — Сайерса [20] для
, (15)
где . На рисунке 11 показан результат расчета ε(2) по этой приближённой формуле (15); оказалось, что среднее отклонение от истинного
. (16)
Эта улучшенная и более компактная формула дает среднюю ошибку в определении
Предположим, что формулу для
, (17)
где , (18)
и где
; (19)
она дает довольно хорошую точность (график с пометкой «Модиф.» на рисунке 11) с относительной погрешностью 5,8 %; но эта погрешность все же больше, чем у формулы (16) («Новый» на рисунке 11).
Приближённые формулы для
Рассмотрим следующую приближённую формулу для
, (20)
где
, (21)
которую предложили авторы статьи [18] и которая в их обозначениях имеет вид:
Предполагая, что первый член
. (22)
Как показано на рисунке 11, графики
Параметры Томсена
По определению (уравнение (5)) выведем аналогичные формулы для параметров Томсена
; ; . (23)
Начнем с параметра Томсена
. (24)
Учитывая, что
. (25)
Затем, домножив числитель и знаменатель дроби на (
. (26)
Для
. (27)
По данным физического моделирования получается, что две поперечные ослабленности
; (28)
. (29)
Заметим, что обе эти формулы для
Интересно, что для
; ; (30)
; . (31)
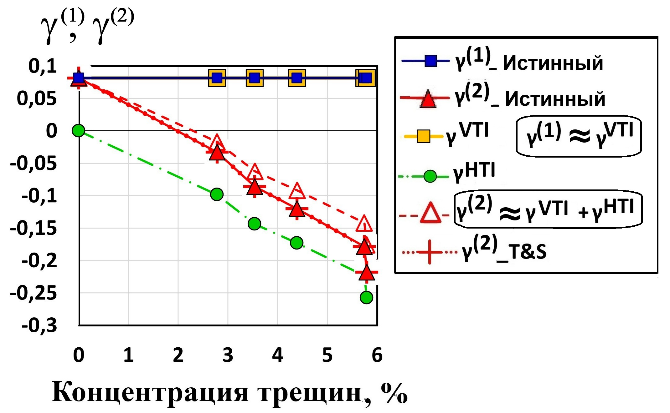
Рисунок 12. Параметры Томсена
Формула сложения VTI + HTI для
Формулу сложения
, (32)
где
Если пренебречь членом
Однако эта формула дает расхождение в 23 % с истинным
δ(
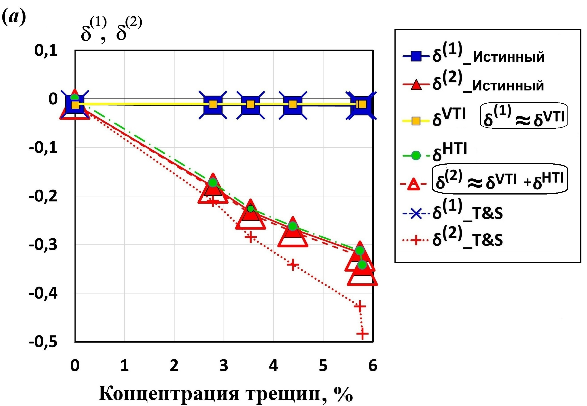
Параметр Томсена
, (35)
, (36)
. (37)
В таблицах 1 и 2 приведены компоненты тензоров ORT, VTI и HTI, т. е. {},
, (38)
получаем его истинное значение «
. (39)
Как это видно на рисунке 13б, эта формула Томсена — Сайерса плохо работает (т. е. средняя относительная разница с истинным
Таким образом, без каких-либо сложных предварительных вычислений орторомбического тензора упругости {
 |
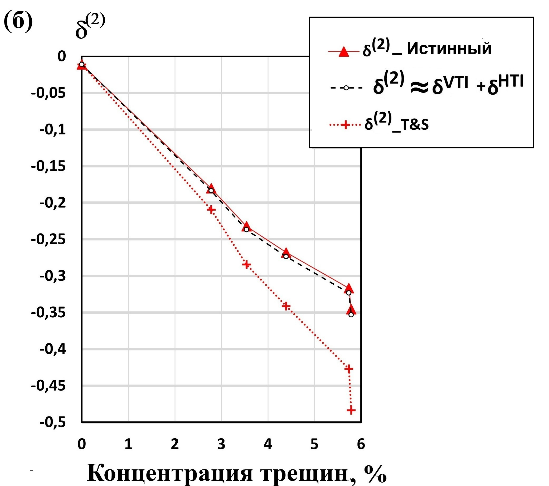 |
Рисунок 13. a) Параметры Томсена
Интересно, что тенденция поведения
Параметр Томсена
. (40)
Как показано на рисунке 13, график «
. (41)
Рисунок 13 показывает, что эта формула
Выводы
Формула сложения ORT = VTI + HTI помогает нам напрямую (без сложных предварительных вычислений) предсказать знак и приблизительную величину искомого параметра Томсена в трещиноватых сланцах (т. е.
Итак, для ε и γ в орторомбической среде ORT имеют место следующие единообразные формулы:
; ;
; .
Что касается формулы сложения ORT = VTI + HTI для
; .
Благодарности
Мы благодарим Мексиканский институт нефти (Instituto Mexicano del Petroleo (IMP)) за поддержку, номер проекта G.72040.
1. Thomsen L. Weak elastic anisotropy / Thomsen L. // Geophysics. — 1986. — № 51. — Pp. 1954–1966. — https://doi.org/10.1190/1.1442051.
2. Grechka V., Tsvankin I. 3-D description of normal moveout in anisotropic inhomogeneous media / Grechka V., Tsvankin I. // Geophysics. — 1998. — № 63. — Pp. 1079–1092. — https://doi.org/10.1190/1.1444386.
3. Chichinina T. Seismic Anisotropy Parameter δ for Fractured Reservoir Characterization Including Gas Saturation / Chichinina T., Mankenov O., Bezkhodarnov V., Avila-Carrera R. // In: Lin, J. (eds). Proceedings of the International Field Exploration and Development Conference 2024. IFEDC 2024. Springer Series in Geomechanics and Geoengineering (SSGG). — Springer, Singapore. — 2025. — Pp. 129–137. —https://doi.org/10.1007/978-981-96-2363-1_10.
4. Горшкалев С. Б. Результаты изучения азимутальной анизотропии геологического разреза на Пеляткинской площади по данным многоволнового ВСП и сейсморазведки 3D / Горшкалев С. Б., Карстен В. В., Афонина Е. В., Бекешко П. С., Корсунов И. В. // Технологии сейсморазведки. — 2011. — № 3. — C. 60–70. EDN: https://elibrary.ru/OKCMGP
5. Чичинина Т. И. Анизотропная модель ORT для газонасыщенных трещиноватых пород / Чичинина Т. И., Детков В. А., Манкенов О. К. // Сборник материалов конференции. «Тюмень — 2024. Актуальные тренды научно-технологического развития нефтегазовой отрасли». — Тюмень. — 2024. — С. 24–27.
6. Чичинина Т. И. Параметр анизотропии δ как индикатор газонасыщенности трещиноватых коллекторов / Чичинина Т. И., Безходарнов В. В., Манкенов О. К. // Сборник материалов конференции. «Геомодель — 2024. 26-я юбилейная научно-практическая конференция по вопросам геологоразведки и разработки месторождений нефти и газа», Россия, Геленджик, 9–12 сентября 2024. — С.114–118. EDN: https://elibrary.ru/RAGLEA
7. Чичинина Т. И. Анизотропия сланцев: орторомбическая модель / Чичинина Т. И., Авила-Каррера Р., Мартюшев Д. А. // Сборник материалов конференции «Наука о сланцах '25. Новые данные». Москва, Россия, 7–8 апреля 2025 г.
8. Chichinina T. Physical bounds on C13 and anisotropy parameter δ for organic mudrocks / Chichinina T., Vernik L. // Geophysics. — 2018. — № 83(5). — Pp. A75 — A79. — https://doi.org/10.1190/geo2018-0035.1 EDN: https://elibrary.ru/YJFFFJ
9. Vernik L. Seismic Petrophysics in Quantitative Interpretation / Vernik L. // Publisher: Society of Exploration Geophysicists (SEG). — 2016. — P. 226. —https://doi.org/10.1190/1.9781560803256.
10. Bakulin A. Estimation of fracture parameters from reflection seismic data —Part I: HTI model due to a single fracture set / Bakulin A., Grechka V., Tsvankin I. // Geophysics. — 2000. — № 65(6). — Pp. 1788–1802. — https://doi.org/10.1190/1.1444863. EDN: https://elibrary.ru/LGBHKJ
11. Vernik L. Velocity anisotropy in shales: a petrophysical study / Vernik L., Liu X. // Geophysics. — 1997. — № 62. — Pp. 521–532. — https://doi.org/10.1190/1.1444162.
12. Chesnokov E. M. Mathematical modelling of anisotropy of illite-rich shale / Chesnokov E. M., Tiwary D. K., Bayuk I. O., Sparkman M. A., Brown R. L. // Geophysical Journal International. — 2009. — № 178(3). — Pp. 1625–1648. — https://doi.org/10.1111/j.1365-246X.2009.04244.x. EDN: https://elibrary.ru/MWYUDD
13. Bayuk I. O. Elastic moduli of anisotropic clay / Bayuk I. O., Ammerman M., Chesnokov E. M. // Geophysics. — 2007. — № 72(5). — P. D107 — D117. —https://doi.org/10.1190/1.2757624. EDN: https://elibrary.ru/KGPBKS
14. Crampin S. A decade of shear-wave splitting in the Earth’s crust: what does it mean? what use can we make of it? and what should we do next? / Crampin S., Lovel J. H. // Geophysical Journal International. — 1991. — № 107. — P. 387–407. —https://doi.org/10.1111/j.1365-246X.1991.tb01401.x.
15. Кашубин С. Н. Сейсмическая анизотропия и эксперименты по ее изучению на Урале и Восточно-Европейской платформе / Кашубин С. Н. — Екатеринбург: УрО РАН, 2001. EDN: https://elibrary.ru/WXCBLP
16. Schoenberg M. Orthorhombic media: modeling elastic wave behavior in a vertically fractured earth / Schoenberg M., Helbig K. // Geophysics. — 1997. — № 62. — P. 1954–1974. — https://doi.org/10.1190/1.1444297.
17. Schoenberg M. Elastic wave behavior across linear slip interfaces / Schoenberg M. // Journal of Acoustical Society of America. — 1980. № 68. — P. 1516–1521. — https://doi.org/10.1121/1.385077.
18. Bakulin A. Estimation of fracture parameters from reflection seismic data — Part II: Fractured models with orthorhombic symmetry / Bakulin A., Grechka V., Tsvankin I. // Geophysics. — 2000. — № 65(6). — P. 1803–1817. — https://doi.org/10.1190/1.1444864. EDN: https://elibrary.ru/LGCHML
19. Silva C. Experimental characterization of synthetic porous orthorhombic fractured medium: A physical modeling approach / Silva C., de Figueiredo J. J. S., Chichinina T., Nascimento M. J., Kirchhof L. // Ultrasonics. — 2019. — № 94. — P. 82–91. — https://doi.org/10.1016/j.ultras.2018.11.015.
20. Thomsen L., Sayers C. Anisotropy parameters for fractured shales / Thomsen L., Sayers C. // Second International Meeting for Applied Geoscience & Energy. Society of Exploration Geophysicists (SEG) and the American Association of Petroleum Geologists (AAPG). — 2022. — P. 150–154. DOI: https://doi.org/10.1190/image2022-3748535.1
21. Chichinina T. Anisotropy Models and Parameters of Fractured Rocks by Physical Modeling Data / Chichinina T., De Figueiredo J. J. S., Bulgakov I., Avila-Carrera R. // In: J. Lin (Ed.). Proceedings of the International Field Exploration and Development Conference 2023. Springer Series in Geomechanics and Geoengineering (SSGG). — Springer Nature. — 2024. — P. 1027–1036. — https://doi.org/10.1007/978-981-97-0468-2_81.
22. Chichinina T. Physical constraints on C13 for transversely isotropic shales and their applications / Chichinina T. // Geophysics. — 2017. — № 82(4). — P. WA105 — WA118. — https://doi.org/10.1190/geo2016-0656.1. EDN: https://elibrary.ru/YGIWIU
23. Schoenberg M. Seismic anisotropy of fractured rock / Schoenberg M., Sayers C. M. // Geophysics. — 1995. — № 60. — P. 204–211. — https://doi.org/10.1190/1.1443748.








