Повышение точности трансформации региональных гравитационных аномалий: учет влияния масс, находящихся за пределами изучаемой площади

Долгаль Александр Сергеевич; Рыжов Никита Валерьевич; Хохлова Валерия Васильевна

doi:doi:

Главная / Журналы / Вестник АГГИ / Повышение точности трансформации региональных гравитационных аномалий: учет влияния масс, находящихся за пределами изучаемой площади

Повышение точности трансформации региональных гравитационных аномалий: учет влияния масс, находящихся за пределами изучаемой площади

Отправить рукопись

Цитировать

Цитирований:

ПОВЫШЕНИЕ ТОЧНОСТИ ТРАНСФОРМАЦИИ РЕГИОНАЛЬНЫХ ГРАВИТАЦИОННЫХ АНОМАЛИЙ: УЧЕТ ВЛИЯНИЯ МАСС, НАХОДЯЩИХСЯ ЗА ПРЕДЕЛАМИ ИЗУЧАЕМОЙ ПЛОЩАДИ

Журнал: ВЕСТНИК АГГИ

Рубрики: ИНЖЕНЕРНАЯ И РУДНАЯ ГЕОФИЗИКА

Долгаль Александр Сергеевич ¹

Рыжов Никита Валерьевич

Хохлова Валерия Васильевна ³

Информация об авторах и публикации

Авторы:

1. Горный институт Уральского отделения РАН (EGPГлавный научный сотрудник)
сотрудник с 01.01.2002 по настоящее время

Уральский государственный горный университет

3. Россия

Тип:

Статья

Страницы:

с 1 по 1

Статус:

Классификаторы:

ВАК 1.6 Науки о Земле и окружающей среде
ВАК 1.2.1 Искусственный интеллект и машинное обучение
ВАК 1.2.2 Математическое моделирование, численные методы и комплексы программ

Язык материала:

русский

Ключевые слова:

гравиразведка, аномалия, трансформация, эквивалентные источники, задача Дирихле, Сибирская платформа.

Финансирование:

Исследование выполнено при финансовой поддержке Министерства науки и высшего образования РНФ в рамках государственного задания (рег. номер НИОКТР: 124020500054-3).

Аннотация и ключевые слова

Аннотация (русский):
Представлена методика трансформации аномалий силы тяжести для больших территорий, в которой используются геодезические координаты точек поля и учитывается сферообразная форма Земли. Разработан новый алгоритм, реализованный в программе TRANSF_VR, написанной на языке Delphi, который является дальнейшим развитием к построению двухуровенных истокообразных аппроксимаций геопотенциальных полей. С целью минимизации краевых эффектов используется два уровня глубин размещения эквивалентных источников (точечных масс): «приповерхностный» и «глубинный», а также две исходные телескопированные цифровые модели гравитационного поля. Параметры источников определяются путем последовательного решения двух систем линейных алгебраических уравнений методами Холецкого и наискорейшего градиентного спуска. Высокую скорость вычислений обеспечивает разрежение сети задания значений поля за пределами территории исследований. Представлены результаты преобразования гравитационного поля в полной редукции Буге (глобальная модель EIGEN-GRGS.RL04.MEAN-FIELD) для Сибирской платформы и обрамляющих ее структур с координатами 52°–72° с. ш., 84°–132° в. д. общей площадью около 5.15 млн км².

Ключевые слова:
гравиразведка, аномалия, трансформация, эквивалентные источники, задача Дирихле, Сибирская платформа.

Текст

Введение

В прикладной геофизике при обработке и интерпретации материалов гравиметрической съемки обычно используется модель «плоской Земли» и отвечающая ей декартова система прямоугольных координат. Значительно реже находит применение при изучении больших территорий модель «сферической Земли» [1]. Некоторые исследователи работают с более сложными моделями «эллипсоидальной Земли», являющимися более точным приближением формы нашей планеты [2].

Рассмотрим экспериментальные оценки различий результатов пересчета аномалий силы тяжести в верхнее полупространство для перечисленных выше моделей. Пересчет на высоту 50 км выполнялся путем подбора масс эквивалентных источников с последующим решением прямой задачи гравиразведки от полученной аппроксимационной конструкции [3]. Эквивалентными источниками во всех случаях являлись шары (точечные массы), находящиеся под точками задания поля на фиксированной глубине h₀, близкой к шагу сети цифровой GRID-модели.

При сопоставлении «плоской» и «сферической» моделей Земли исходными данными являлись цифровые GRID-модели гравитационного поля $Δ$ g в редукции Буге и нормальных высот рельефа земной поверхности в пределах листа О-40 карты 1:1 000 000 масштаба (Пермский край). Это предельный размер территории (т. н. сферического двуугольника), при котором целесообразно использовать систему плоских прямоугольных координат Гаусса — Крюгера и соответствующую ей модель Земли. Сеть точек составила 8 $×$ 8 км, размер матриц — 63 строки, 53 столбца. Глубина источников h₀ = 9.6 км, при этом была достигнута точность решения СЛАУ F2 = 0.001 мГал.

Плановое расположение точек поля было одинаковым для обеих моделей Земли, но в первом случае уровенной поверхностью являлась горизонтальная плоскость z = 0, во втором — фрагмент поверхности сферы, обладающей радиусом R = 6371.1 км. Две этих уровенных поверхности соприкасались между собой в юго-западном углу территории. Шар радиуса 6371.1 км по своим размерам, площади поверхности и объему близок к земному эллипсоиду. Для «плоской» Земли аномалии силы тяжести отвечают вертикальной производной V_Z гравитационного потенциала V, которую обычно принято обозначать $Δ$ g. Для модели «сферической» Земли используется уже радиальная производная потенциала V_R. Соответственно, пересчет поля выполнялся на плоскость z = 50 км и на сферу радиусом R = 6421.1 км, а также определялись значения разностного поля δ = V_R - V_Z (таб. 1, рис. 1).

Разностное поле характеризуется среднеквадратическим отклонением (СКО) $~$ 3.4 % от СКО полей на высоте 50 км, диапазон его изменения составляет $~$ 4.6 % от размаха каждого из этих полей. Таким образом, можно говорить о значимых различиях результатов трансформации аномалий силы тяжести, полученных в рамках «плоской» и «сферической» моделей Земли. Степень отличия модели «сферической Земли» от эллипсоида Красовского существенно ниже: СКО разностного поля $δ$ составляет $~$ 0.04 % от СКО аномалий силы тяжести на высоте 50 км, а диапазон изменения $δ$ не превышает $~$ 0.08 % [4].

Более точное приближение к форме Земли обеспечивает сфера В. В. Каврайского с радиусом R = 6372.9 км. Напомним, что при использовании «сферических» моделей Земли долгота L остается неизменной, но происходит замена геодезической широты B на геоцентрическую широту Ф. Направление силы тяжести теперь отвечает радиус-вектору, а не нормали $l$ к поверхности эллипсоида. Для перехода от геодезической широты к геоцентрической используется формула: $Ф = B - 8' 39'' sin 2B$ [5]. Использование «квазиэллипсоидальной Земли» — сферы Каврайского (при замене Ф на кошироту $ϕ$ ) позволяет существенно ускорить вычислительный процесс, т. к. в этом случае не требуется перехода к топоцентрической системе координат в каждой точке задания поля [6].

Таблица 1. Характеристики полей «плоской» и «сферической» моделей Земли на высоте 50 км

Модель Земли	Статистические параметры, мГал
Модель Земли	Минимум	Максимум	Среднее	СКО
«Плоская Земля»	- 11.426	14.344	1.422	5.875
«Сферическая Земля»	- 11.418	14.290	1.594	5.854
Разностное поле	- 0.626	0.589	0.120	0.199

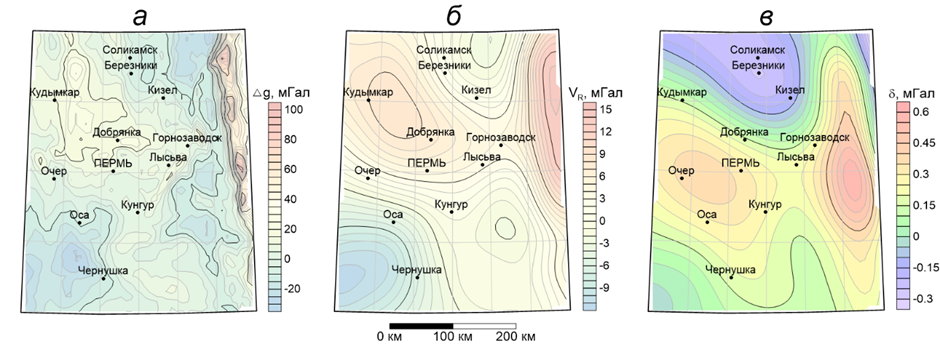
Рисунок 1. Оценка различий моделей «плоской» и «сферической» Земли: а — гравитационное поле $Δ$ g на земной поверхности; б — гравитационное поле V_Rна высоте 50 км; в — разностное поле $δ$ . Лист карты О-40 (Пермский край)

Однако научно обоснованный выбор модели Земли не снимает всех сложностей, возникающих при трансформации региональных аномалий силы тяжести V_R. Речь идет об учете влияния гравитационного эффекта масс, которые находятся за пределами территории исследований, а также о решении систем линейных алгебраических уравнений (СЛАУ) большой размерности с приближенно заданной правой частью. Далее в статье будут рассмотрены вопросы, связанные с этими сложностями.

Учет влияния сторонних масс

Имеются многочисленные примеры, свидетельствующие о том, что разные пространственные распределения эквивалентных источников, одинаково хорошо аппроксимирующие аномалии силы тяжести на поверхности Земли, могут генерировать заметно различающиеся между собой значения трансформант [7]. С математической точки зрения это объясняется использованием интеграла Пуассона для решения внешней задачи Дирихле при конечных пределах области интегрирования и дискретном характере задания значений поля. В большинстве случаев наиболее заметные искажения трансформант возникают на периферии области задания поля D₁, их можно назвать краевыми эффектами.

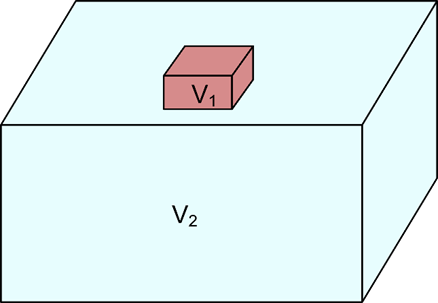
В идеале избежать краевых эффектов можно при построении аппроксимационной конструкции, полностью адекватной реальному распределению аномалиеобразующих масс (плотности) в геологической среде, причем в объеме V₂, существенно превышающем размер изучаемого фрагмента V₁, V₁ ⊂ V₂ (рис. 2). На практике этого достичь невозможно, т. к., начиная с какого-то объема петрофизической информации, «лишаются смысла гравиразведочные (магниторазведочные) работы, цель которых состоит в изучении распределения плотности (намагниченности) в геологической среде» [8].

Рисунок 2. Схема, поясняющая соотношение между объемом V₁, содержащим аномалиеобразующие массы, и изучаемым фрагментом геоплотностной среды V₂

С целью минимизации краевых эффектов предлагается использовать два уровня глубин размещения эквивалентных источников (точечных масс): «приповерхностный» и «глубинный», а также информацию, относящуюся к самой области D₁ и к существенно превышающей ее по площади сопредельной территории D₂. Имеются примеры современных исследований, доказывающие возможность повышения точности расчета трансформант при размещении точечных масс на разных глубинах h от земной поверхности, в частности — работа [9]. Совокупность значений и пространственных координат этих масс представляет собой аналитическую модель интерпретируемого гравитационного поля V_R (рис. 3). Высокая скорость вычислений обеспечивается за счет разрежения сети задания значений поля в пределах области D₂ ⊃ D₁.

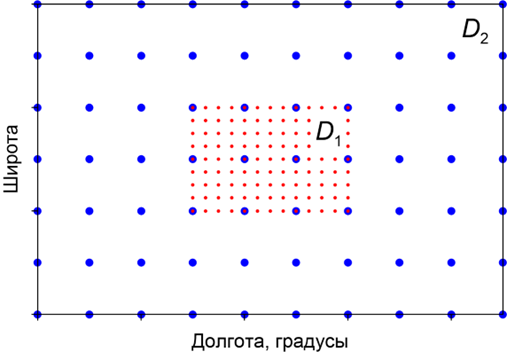
Рисунок 3. Схема расположения точечных масс в аналитической модели гравитационного поля: красный цвет — «приповерхностные» источники с глубиной h₁, синий цвет — «глубинные» источники с глубиной h₂ > h₁

Этот способ не является новым [10], но он использовался лишь для построения «локальных аппроксимаций» (термин В. Н. Страхова) в прямоугольной системе координат. В данном случае под линейной трансформантой функции $u(φ, λ, R)$ подразумевается новая функция $v(φ, λ, R)$ , определенная на произвольной поверхности S в пределах области D₁:

$v\left( \varphi,\lambda,R \right) = T\left\{ u\left( \varphi,\lambda,R \right) \right\} = T\left\{ u_{1}\left( \varphi,\lambda,R \right) \right\} + T\left\{ u_{2}\left( \varphi,\lambda,R \right) \right\},$ (1)

где Т — некоторый линейный оператор трансформации, а функция $u$ представляет собой сумму двух составляющих: $u = u_1 + u_2$ , где $u_1$ — модельное поле V_R «глубинных» масс, а $𝑢_2$ — разность наблюденного и модельного полей внутри области исследований D₁.

Определение значений масс эквивалентных источников

Массы эквивалентных источников определяются с помощью решения системы линейных алгебраических уравнений (СЛАУ) с приближенно заданной правой частью вида:

$Gm = u$ , (2)

где G — квадратная матрица значений гравитационных эффектов элементарных источников с единичной массой (m = 1), m — вектор неизвестных значений аномальных масс, u — вектор значений аномального гравитационного поля V_R в редукции Буге. Под гравитационным эффектом в данном случае подразумевается 1-я радиальная производная гравитационного потенциала точечного источника $V_{R}\left( R_{0},\varphi_{0},\lambda_{0} \right) = f\frac{\left( R_{0} - \text{rcosω} \right)}{r_{0}^{3}}$ , где $f = 6.67 × 10^{-11} м^3⋅кг^{-1}⋅с^{-2}$ — гравитационная постоянная, $R_0, φ_0, λ_0$ — координаты точки измерений, $r, φ, λ$ — координаты источника, $r_{0} = \sqrt{R_{0}^{2} + r^{2} - 2R_{0}\text{rcosω}}$ , $ω$ — угол при центре O земного шара между точкой измерений и источником: $сosω = cosφ_0cosφ + sinφ_0sinφ cos cos (λ_0 - λ)$ . По сути осуществляется решение линейной обратной задачи гравиразведки [11], в котором искомые значения масс (плотностей) m не используются для получения новой геологической информации, а являются лишь средством для восстановления аномалий силы тяжести u в произвольно выбранных точках пространства, а также обеспечивают высокоточный расчет трансформант v.

На первом этапе аппроксимации выполняется определение значений «глубинных» точечных масс, обеспечивающих минимум среднеквадратического расхождения исходного и модельного полей во всех имеющихся точках поля (совпадающие точки областей D₁ и D₂ исключаются). Для этой цели формируется нормальная СЛАУ $G^{T} G α = G^{T} u$ , решение которой осуществляется методом Холецкого [12]. Эта система всегда совместна, матрица ее коэффициентов G^TG обладает свойством симметричности и положительной определенности (т. н. матрица SPD — Simmetric and Positively Defined). Однако обусловленность ее несколько ухудшается: $\sqrt{c o n d G^{T} G} = c o n d G .$ Приблизительные потери в точности решения при выполнении условия h ≅ ΔL , где ΔL — расстояние между точками задания поля, могут достигать 5–6 значащих цифр. Это существенно ниже критических значений. В частности, для компьютера автора статьи Asus Aspire VN7-791 с процессором Intel(R) Core(TM) i7-4710HQ экспериментально определенное значение машинного нуля $ε_{0} ≅ 1 \times 10^{- 19}$ , т. е. при таких потерях результаты ориентировочно будут содержать не менее 12 значащих цифр.

На втором этапе гравитационный эффект разности исходных значений поля и поля «глубинных» источников в пределах области D₁ аппроксимируется системой «приповерхностных» точечных масс, значения которых определяются путем решения СЛАУ итерационным методом наискорейшего градиентного спуска (НГС) [12]. В процессе решения используется предварительно рассчитанный массив коэффициентов системы G ̃, хранящийся в оперативной памяти (RAM) компьютера. Он представляет собой разреженную матрицу, сформированную с учетом резкого уменьшения амплитуды гравитационного поля по мере удаления от точечного источника, которая на расстояниях в (15–25) h принимается равной нулю. Для гридированных данных о поле $u_{kl}$ }, $k = \overset{\overline{}}{1,m}, l = \overset{\overline{}}{1,n}$ определение косинуса угла при центре Земли между точкой измерений поля и точечной массой $сosω = cosφ_0cosφ + sinφ_0sinφ cos(λ_0 - λ)$ можно существенно ускорить. Для этого достаточно однократно рассчитать $m$ значений $cosφ$ и $n$ значений $cos(λ_0 - λ)$ , а затем сохранить их в одномерных массивах вещественных чисел [13].

Выбор относительных глубин h источников, равных шагу сети задания поля по меридиану для двух цифровых моделей поля V_R, обеспечивает достаточно хорошую обусловленность СЛАУ. Это влечет за собой высокую скорость сходимости для метода НГС. По оценке авторов доклада данный принцип погружения источников не может использоваться лишь для площадей, расположенных в полярных областях Земли, за пределами широты 70°. После определения значений всех точечных масс для вычисления трансформант v в формуле (1) могут применяться различные линейные операторы T. Пересчет гравитационного поля V_Rна фрагмент внешней по отношению к Земле сферической поверхности с радиусом R' = R₀ + H, где H — нормальная высота, в данном случае отвечает приведению поля V_Z на горизонтальную плоскость z = const для «плоской Земли». Данный алгоритм реализован в программе TRANSF_VR [14], которая позволяет осуществлять вычисление первой радиальной производной гравитационного потенциала V_R, гравитационного потенциала V, его вторых производных $V_{Rλ}$ , $V_{Rϕ}$ и модуля горизонтального градиента Gr на земной поверхности и на заданной высоте H (рис. 4). Для корректного использования производных $𝑉_{𝑅𝜆}, 𝑉_{𝑅𝜙}$ при вычислении горизонтального градиента аномалий силы тяжести Gr необходимо дополнительно использовать коэффициенты Ламе для сферической системы координат $τ_1=1⁄(R_{0} sin⁡φ)$ и $τ_2=1⁄R_0$ : $Gr=(τ_1 V_{Rλ}^2+τ_2 V_{Rφ}^2 )^0.5$ .

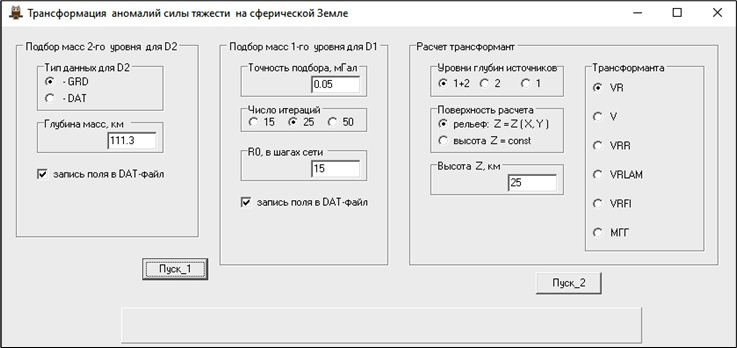
Рисунок 4. Главное окно программы TRANSF_VR

Трансформация аномалий силы тяжести Сибирской платформы и обрамляющих ее структур

В качестве примера работы программы TRANSF_VR возьмем данные глобальной модели гравитационного поля EIGEN-GRGS.RL04.MEAN-FIELD, полученной на основе данных спутниковых миссий GRACE и SLR в 2019 г. Используется цифровая модель аномалий силы тяжести в полной редукции Буге с плотностью промежуточного слоя 2.67 г/см³ для территории, ограниченной 52°–72° с. ш., 84°–132° в. д.

Область D₁ размером $~$ 5.15 млн. км² охватывает всю Сибирскую платформу и структуры ее обрамления. Шаг сети — 0.1°, размерность GRID-модели — 201 × 486 (N = 97 686 точек). Источником информации о рельефе земной поверхности являлась модель ETOPO1. Диапазон изменения аномалий силы тяжести $~$ 387 мГал, высотные отметки H лежат в пределах от - 19 до 2868 м. Эквивалентные источники располагаются на 11.13 км ниже земной поверхности. Поле в области D₂ с координатами 5°–80° с. ш., 15°–180° в. д. задано с шагом 5°. Относительная глубина h точечных масс составляет 550 км (рис. 5).

После выполнения 50 итераций методом НГС была достигнута точность аппроксимации аномалий силы тяжести $~$ 0.17 мГал в евклидовой метрике F2, что превосходит точность исходных материалов [15]. Время решения задачи составило 758 с., вычисления проводились на компьютере среднего класса OptiPlex 7070, при этом около 50 % затрат машинного времени занял ввод/вывод исходных данных и результатов расчета.

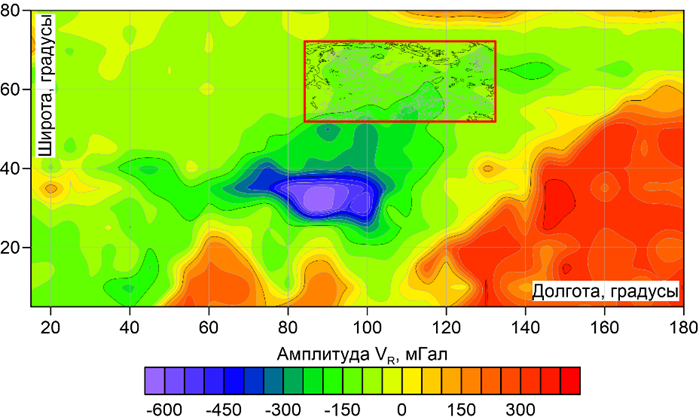
Рисунок 5. Совмещенные карты изоаномал гравитационного поля для областей D₁ и D₂: красный контур — территория исследований D₁

После определения параметров двух разноглубинных систем точечных масс для вычисления трансформант v могут применяться различные линейные операторы T. Пересчет гравитационного поля V_R на фрагмент внешней по отношению к Земле сферической поверхности с радиусом R' = R₀ + H, где H — нормальная высота, в данном случае отвечает приведению поля V_Z на горизонтальную плоскость z = const для «плоской Земли». Аналогом вертикальной производной силы тяжести V_ZZ является вторая радиальная производная силы тяжести V_RR. Соответствующую аналогию можно также провести между вторыми производными V_ZX, V_ZY и V_Rλ, V_Rφ. Вторые производные гравитационного потенциала характеризуют скорость изменения силы тяжести в пространстве и отражают локальные особенности геологического строения. Для корректного использования производных V_Rλ , V_Rφ при вычислении горизонтального градиента аномалий силы тяжести Gr необходимо дополнительно использовать коэффициенты Ламе для сферической системы координат $𝜏_ 1 = 1 ⁄ ( 𝑅_ 0 𝑠 𝑖 𝑛 ⁡ 𝜑 )$ $𝜏1 = 1 ⁄ ( 𝑅_ 0 𝑠 𝑖 𝑛 ⁡ 𝜑 )$ и $𝜏_ 2 = 1 ⁄ 𝑅_ 0$ : $𝐺 𝑟 = ( 𝜏_ 1 𝑉_ {𝑅 𝜆}^ 2 + 𝜏_ 2 𝑉_ {𝑅 𝜑}^ 2 )^ 0.5$ .

Сопоставим представленные на 50-й сессии семинара им. Д. Г. Успенского — В. Н. Страхова результаты пересчета гравитационного поля V_R в верхнее полупространство на высоту Н = 250 км [16] c новыми данными, полученными при двух уровнях размещения эквивалентных источников. Для графического отображения данных (рис. 6), как и ранее, использована равноугольная нормальная коническая проекция (НКП), в которой меридианы изображаются прямыми, сходящимися в общей точке под углами, пропорциональными разности долгот, а параллели изображаются концентрическими окружностями, имеющими общий центр в точке пересечения меридианов [17]. Параметры НКП: главная параллель 62°, центральный меридиан 108°. Как можно заметить, недостаток суммарной массы источников на периферии территории привел к появлению артефактов — замыканию изолиний вблизи ее южной границы (рис. 6а). Наличие «глубинных» масс повлекло за собой существенное изменение амплитудных характеристик аномалий силы тяжести при пересчете на высоту (рис. 6б).

В системе КОСКАД 3D [18] выполнялся интеллектуальный анализ результативного набора трансформант с использованием вероятностно-статистических методов. С целью трассирования аномалий гравитационного поля на высоте Н = 25 км различных энергий и различного направления применялась оригинальная модификация одномерной адаптивной фильтрации. Выделенные оси положительных и отрицательных аномалий, связанные преимущественно с дизъюнктивной тектоникой, показаны на рисунке 7а. С помощью двухмерной энергетической фильтрации были выделены различные составляющие этого поля, наиболее энергоемкая из них (тренд) приведена на рисунке 7б. Морфология этой составляющей отражает наиболее крупные тектонические элементы Сибирской платформы и неоднородное по плотности строение верхней мантии под ней.

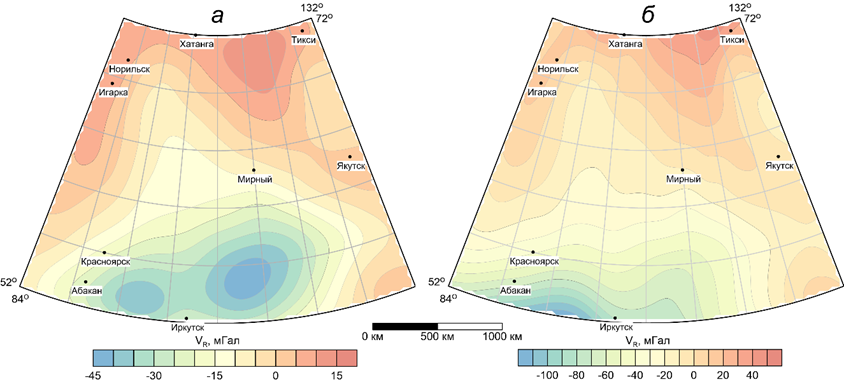
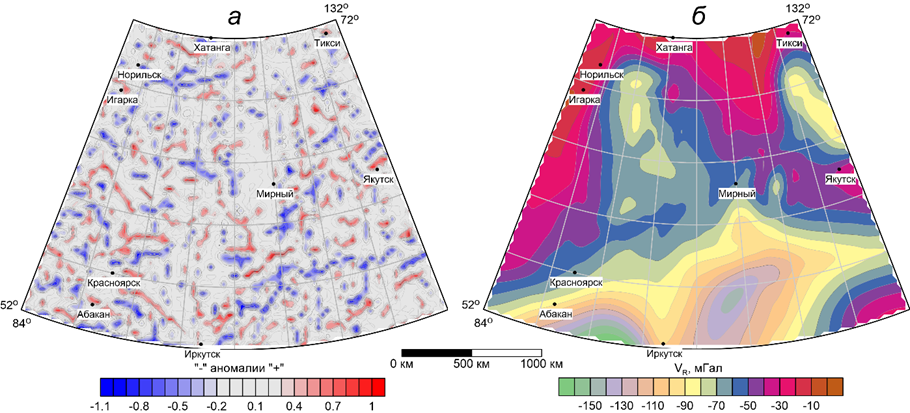
Рисунок 6. Карты изоаномал силы тяжести V_R в редукции Буге на высоте 250 км, полученные путем пересчета поля в верхнее полупространство при одном (а) и двух (б) уровнях размещения точечных масс

Рисунок 7. Результаты автоматического трассирования осей аномалий (а) и наиболее энергоемкая составляющая гравитационного поля V_R (б)

Объемное распределение эффективного параметра, пропорционального плотности горных пород, построено в системе КОСКАД 3D с применением статистических, спектрально-корреляционных методов и алгоритма адаптивной фильтрации в окне живой формы на основе преобразования Б. А. Андреева. Блок-диаграмма квазиплотности (рис. 8) представляет собой результат перехода от 2D- к 3D-геоизображениям на основе аналитических компьютерных процедур логико-математической генерализации. Последовательное повышение уровня генерализации обеспечивает проявление на геоизображениях элементов все более крупных геосистем, что способствует выявлению качественно новой информации и закономерностей. Построенная блок-диаграмма характеризует основные особенности глубинного строения Сибирской платформы и обрамляющих ее структур, в т. ч. слабо проявленные в наблюденном гравитационном поле.

Результаты свертки информации методом компонентного анализа по 7 признакам (гравитационное поле на высоте 25 км, модуль горизонтального градиента на той же высоте, 2-я радиальная производная гравитационного потенциала на высоте 75 км, 4 компоненты разложения поля методом энергетической фильтрации) приведены на рисунке 9. Пространственное распределение 1-й главной компоненты имеет отчетливо выраженную взаимосвязь с известными тектоническими структурами Сибирской платформы — Енисей-Хатангским перикратонным прогибом, Тунгусской и Вилюйской синеклизами, Алдано-Становым щитом и др.

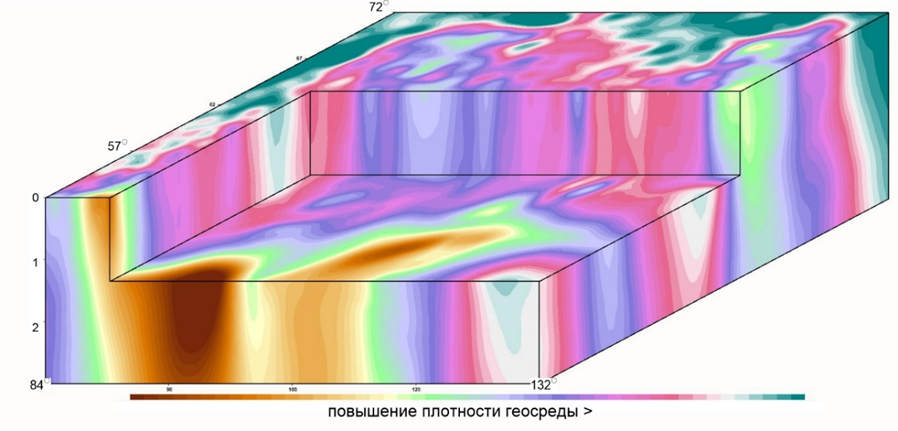
Рисунок 8. Блок-диаграмма относительного распределения плотности в литосфере

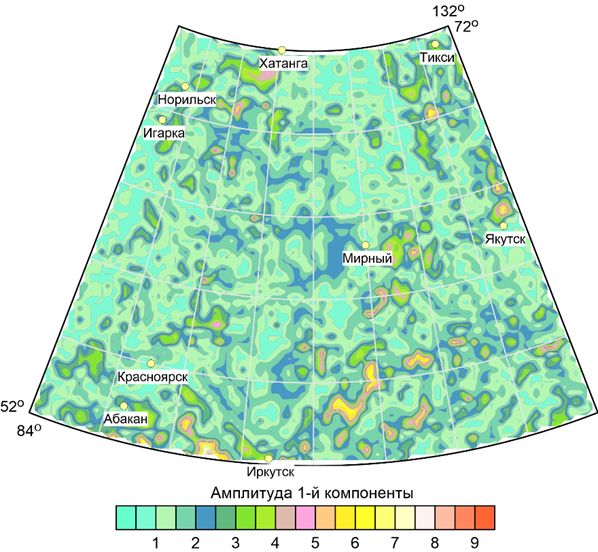
Рисунок 9. Карта 1-й главной компоненты, включающей в себя 7 признаков — трансформант гравитационного поля

Выводы

Разработана компьютерная технология трансформации аномалий силы тяжести в пределах больших территорий, в которой используются «квазиэллипсоидальная» модель Земли — сфера Каврайского и геодезические координаты точек задания поля. При вычислениях используются две телескопированные цифровые модели гравитационного поля с разным шагом сети при двух уровнях размещения точечных масс — «глубинном» и «приповерхностном». Это позволяет уменьшить негативные эффекты, проявляющиеся при одной глубине размещения эквивалентных источников и обеспечивает высокую скорость вычислительного процесса. Результативный набор трансформант, представленных в цифровой форме, может использоваться для интеллектуального анализа в системе КОСКАД 3D методами интерпретационной томографии, автоматизированной классификации и распознавания образов. Также предварительно может осуществляться геологическое редуцирование интерпретируемого гравитационного поля.

Благодарности

Исследование выполнено при финансовой поддержке Министерства науки и высшего образования РФ в рамках государственного задания (рег. номер НИОКТР: 124020500054-3).

Список литературы

1. Глазнев В. Н. Мощность земной коры территории Республики Нигер по данным стохастической интерпретации гравитационного поля / Глазнев В. Н., Якуба И. А. // Вестник Воронежского государственного университета. Серия: Геология. — 2020. — № 4. — С. 46–58. — DOI:https://doi.org/10.17308/geology.2020.4/3126.

2. Страхов В. Н. Метод S-аппроксимаций и его использование при решении задач гравиметрии (региональный вариант) / Страхов В. Н., Степанова И. Э. // Физика Земли. — 2002. — № 7. — С. 3–12.

3. Аронов В. И. Методы построения карт геолого-геофизических признаков и геометризация залежей нефти и газа на ЭВМ / Аронов В. И. — М.: Недра, 1990.

4. Долгаль А. С. Выбор модели Земли для трансформации аномалий силы тяжести в процессе региональных исследований / Долгаль А. С., Костицын В. И., Пугин А. В., Хохлова В. В. // Геофизика. — 2022. — № 5. — С. 6–12. — DOI:https://doi.org/10.34926/geo.2022.55.36.001.

5. Белкин А. М. Воздушная навигация: справочник / Белкин А. М., Миронов Н. Ф., Рублев Ю. И., Саранский Ю. Н. — М.: Транспорт, 1988.

6. Торге В. Гравиметрия / В. Торге; пер. с англ. Г. А. Шанурова, под ред. А. П. Юзефович. — М.: Мир, 1999.

7. Пугин А. В. Истокообразные аппроксимации геопотенциальных полей. От теории к практике / Пугин А. В. // Геофизические исследования. — 2018. — Т. 19. — № 4. — С. 16–30. — DOI:https://doi.org/10.21455/gr2018.4-2.

8. Результаты применения моделирования в рудной геофизике в различных районах Сибири / под ред. В. С. Моисеева, Г. Г. Ремпеля. — М.: Недра, 1988.

9. Li D. A Dual-Layer Equivalent-Source Method for Deriving Gravity Field Vector and Gravity Tensor Components from Observed Gravity Data / Li D., Liang Q., Du J., Chen C. // Pure and Applied Geophysics. — 2022. — Vol. 179. — № 6. — Pp. 2273–2288. — DOI:https://doi.org/10.1007/s00024-022-03047-3.

10. Патент № 2431160 C1. Российская Федерация, МПК G01V 7/06. Способ построения трансформант гравитационного поля: № 2010101347/28: заявл. 18.01.2010: опубл. 10.10.2011 / С. Г. Бычков, А. С. Долгаль, А. В. Пугин, Н. В. Веселкова; заявитель Учреждение Российской академии наук Горный институт Уральского отделения РАН (ГИ УрО РАН).

11. Ягола А. Г. Обратные задачи и методы их решения. Приложения к геофизике / Ягола А. Г., Ван Янфей, Степанова И. Э., Титаренко В. Н. — М.: БИНОМ, Лаборатория знаний, 2014.

12. Бахвалов Н. С. Численные методы / Бахвалов Н. С., Жидков Н. П., Кобельков Г. М. — М.: Наука, 2000.

13. Долгаль А. С. Моделирование аномалий силы тяжести системой точечных масс на сфероообразной Земле / Долгаль А. С., Костицын В. И., Новикова П. Н., Пугин А. В. // Геофизика. — 2023. — № 5. — С. 10–17. — DOI:https://doi.org/10.34926/geo.2023.13.94.002.

14. Свидетельство о государственной регистрации программы для ЭВМ № 2024685961 Российская Федерация. Программа для трансформации региональных аномалий силы тяжести «TRANSF_VR»: № 2024684494: заявл. 18.10.2024: опубл. 02.11.2024 / А. С. Долгаль, Н. В. Рыжов, В. В. Хохлова; заявитель Федеральное государственное бюджетное учреждение науки Пермский федеральный исследовательский центр Уральского отделения Российской академии наук.

15. Конешов В. Н. Сравнение современных глобальных ультравысокостепенных моделей гравитационного поля Земли / Конешов В. Н., Непоклонов В. Б., Соловьев В. Н., Железняк Л. К. // Геофизические исследования. — 2019. — Т. 20. — № 1. — С. 13–26. — DOI:https://doi.org/10.21455/gr2019.1-2.

16. Долгаль А. С. Трансформации региональных аномалий силы тяжести с использованием эквивалентных источников / Долгаль А. С., Новикова П. Н. // Вопросы теории и практики геологической интерпретации гравитационных, магнитных и электрических полей. Материалы 50-й юбилейной сессии Международного семинара им. Д. Г. Успенского — В. Н. Страхова. — М: ИФЗ РАН, 2024. — С. 144–148.

17. Лебедев П. П. Картография: Учебное пособие для вузов / Лебедев П. П. — М.: Академический проспект; Трикста, 2017.

18. Петров А. В. Компьютерная технология статистического и спектрально-корреляционного анализа данных КОСКАД 3D и практические результаты / Петров А. В., Демура Г. В., Зиновкин С. В. // Недропользование XXI век. — 2017. — № 1 (64). — С. 44–59.