Россия
Россия
В статье рассматривается метод моделирования направления траектории бурения горизонтальной скважины на основе искусственного интеллекта Differential Evolution для решения проблем с оптимизацией в ограниченных условиях. Этот метод выполняется путем генерации решений для увеличения вероятности достижения наилучшего горизонтального бурения с максимальным нефтеизвлечением, что позволит уменьшить количество эксплуатационных расходов за счет сокращения штата сотрудников, проведения прогнозной аналитики и комплексной оптимизации уровня активов, а также позволит уменьшить время на реализацию проекта. Сначала строится модель пласта и подвергается предварительной обработке, чтобы избежать влияния ошибок измерения и аномальных помех. Затем компилируется код с помощью Python для прогнозирования наилучшей траектории ствола скважины.
Дифференциальная эволюция; создание начальной популяции; генерация решения методом мутации; генерация решения методом кроссинговера; псевдокод дифференциальной эволюции; траектории расположения горизонтальных участков скважины; создание оптимальной траектории скважины.
Общие сведения о месторождении
В соответствии с принятой схемой нефтегазогеологического районирования Сибирской платформы, нефтегазоконденсатное месторождение относится к Лено-Тунгусской нефтегазоносной провинции, Непско-Ботуобинской нефтегазоносной области, Ботуобинскому нефтегазоносному району.
Геологический разрез района характеризуют нижнепротерозойские образования кристаллического фундамента и рифейские, вендские, кембрийские, юрские, четвертичные отложения осадочного чехла. Основную роль в строении осадочного чехла играют терригенно-карбонатные отложения венда и галогенно-карбонатные образования кембрия.
В тектоническом отношении нефтегазоконденсатное месторождение находится в северо-восточной части Непского свода, осложняющего Непско-Ботуобинскую антеклизу, в зоне сочленения его с Мирнинским выступом и Нюйско-Джербинской впадиной Предпатомского прогиба (рис. 1).
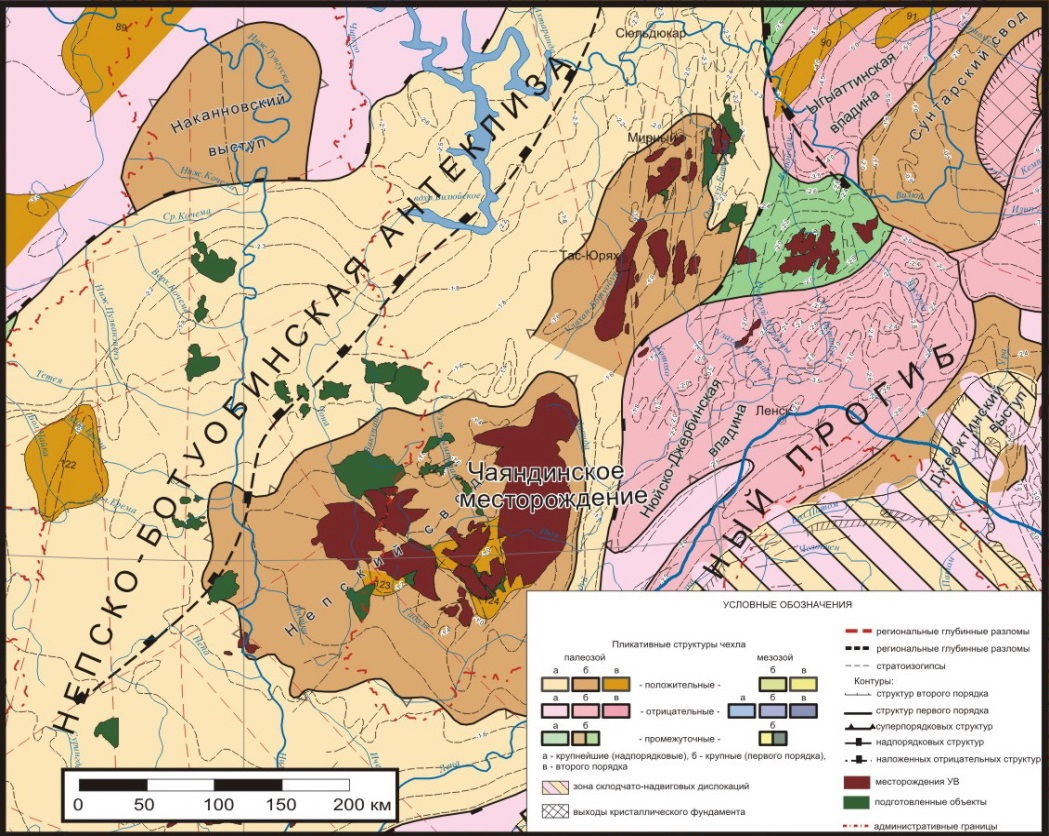
Рисунок 1. Структурно-тектоническая карта северо-восточной части Непского свода
Рассматриваемое месторождение приурочено к одноименному блоку и отделяется от примыкающего к нему Талаканского месторождения грабеном.
Блок Х расположен к востоку от Талаканского блока, в пределах Непского свода юго-восточного склона. С запада и юго-востока он ограничен системой клинообразно сходящихся к югу разломов субмеридионального и северо-западного направлений.
Блок Х с запада ограничен региональным разломом. Он прослеживается на расстоянии более 100 км: от осевой части Непского свода к Нюйско-Джербинской впадине. Амплитуда разлома в отложениях венда и нижнего кембрия практически одинакова и изменяется только по простиранию от 10 до 50 м [1].
С юга и юго-востока блок ограничен разломом северо-восточного простирания, по которому проходит граница надпорядковых структур: Непско-Ботуобинской антеклизы и Предпатомского прогиба. Разлом наиболее уверенно выделяется в осадочном чехле, отчетливо отображается в геофизических полях и картируется на поверхности геологической съемкой.
Оба региональных разлома являются не только границами блока, но и контролируют местоположение залежей месторождения.
Наиболее протяженный в пределах блока разлом выделяется на юго-восточном склоне. Он прослеживается на расстоянии 115 км с юго-запада (от субмеридионального грабена) на северо-восток, образуя Южный и Саманчакитский блоки (рис. 2).
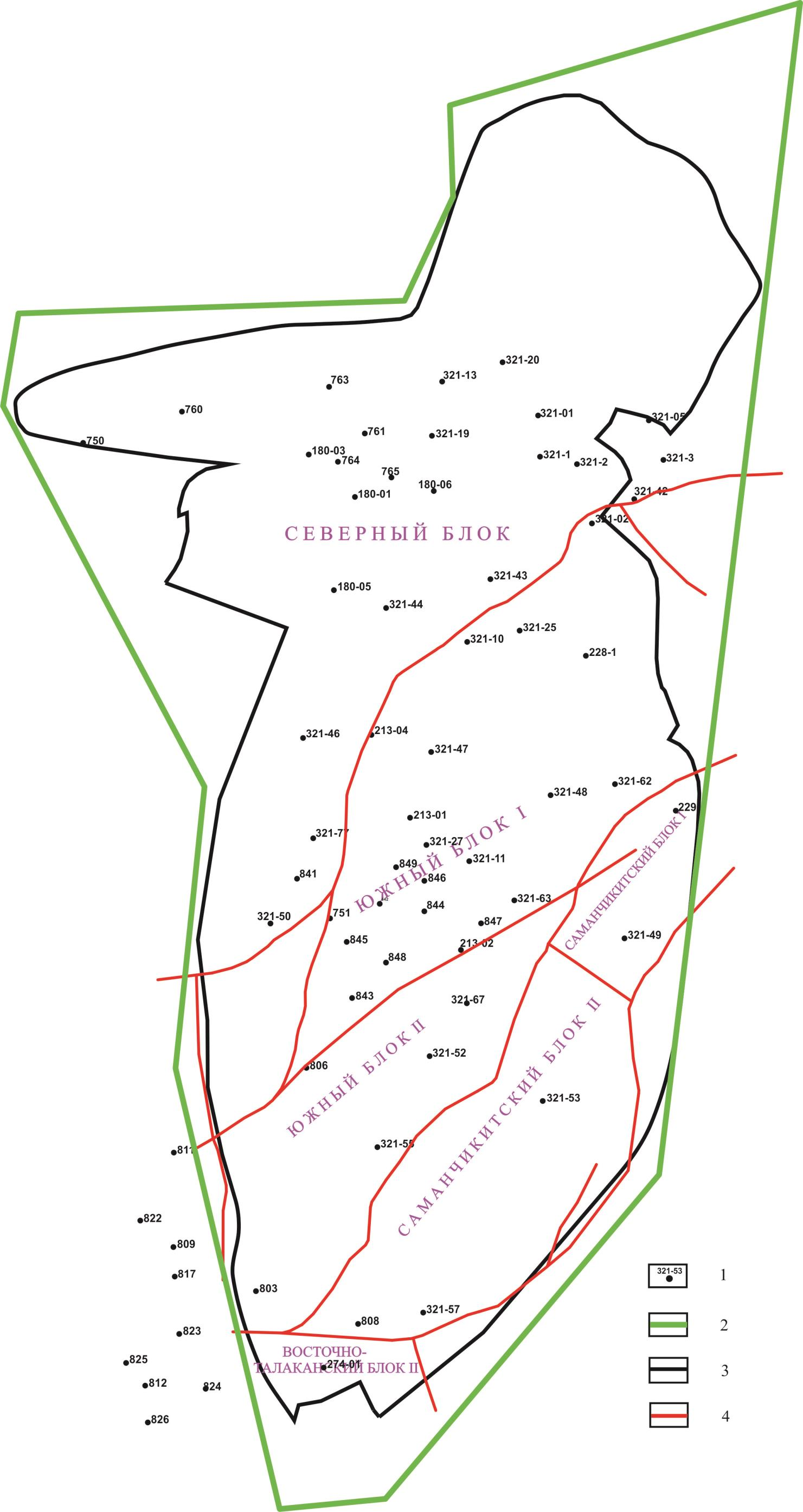
Рисунок 2. Схема блокового строения нефтегазоконденсатного месторождения [3]: 1 – пробуренные скважины; 2 – граница лицензионного участка; 3 – контуры НГКМ; 4 – обозначение разломов
Саманчакитский блок на юго-западе ограничивается субмеридиональным дизьюнктивным нарушением, которое отделяет его от Восточно-Талаканского блока. В пределах последнего расположена скважина № 274-01, прослеживается на расстоянии около 25 км и имеет амплитуду порядка 20 м [2].
Саманчакитский блок приподнят относительно Восточно-Талаканского и Южного.
На севере и северо-востоке блок осложняется системой малоамплитудных (10–20 м) разломов северо-западного и северо-восточного направлений, образующих Северный блок, расположенный в периклинальной части Непско-Пеледуйского свода, и Южный.
В юго-западной части Южного блока по материалам сейсморазведки и электроразведки выделяется разлом северо-западного простирания, который разделяет вышеупомянутый блок на два блока: Южный-I и Южный-II. Амплитуда разлома до 50 м, протяженность – 20 км. Расположенный на юго-западе блок Южный-II является относительно погруженным.
Промышленные скопления нефти и газа в целом по району известны в широком диапазоне разреза от подсолевого карбонатного комплекса венд-нижнего кембрия (осинский горизонт (пласты О-I и O-II) [4] и юряхский (пласты Ю-I, Ю-II)) до терригенной базальной толщи венда (ботуобинский, харыстанский, улаханский, хамакинский, талахский и вилючанский горизонты).
В пределах месторождения промышленные скопления углеводородов выявлены в трех горизонтах – ботуобинском, хамакинском и талахском. Вилючанский горизонт также продуктивен на ограниченной площади, но по строению газовой залежи составляет единый резервуар с талахским горизонтом. Основные залежи в этих горизонтах в разной степени разведаны, а запасы углеводородов учтены в государственном балансе.
В строении и нефтегазоносности терригенных продуктивных горизонтов главную роль играют структурный и литологический факторы.
В условиях преимущественного моноклинального залегания продуктивных отложений структурообразующими являются многочисленные разрывные нарушения. Сквозные разломы, затрагивающие весь осадочный разрез, встречаются относительно редко. Одни дизъюнктивы развиты в кристаллическом фундаменте и низах осадочного чехла, затухая вверх по разрезу, другие, наоборот, затрагивают лишь верхнюю часть разреза. Наряду с субвертикальными разломами отмечается наличие пологих надвигов, которые в пределах рассматриваемой зоны приурочены, как правило, к верхам галогенно-карбонатного разреза.
В строении всех выявленных здесь залежей решающую роль имеет литологический фактор. Коллекторы продуктивных горизонтов выклиниваются и замещаются. Это относится как к терригенным коллекторам, так и к карбонатным.
Совместное проявление структурного и литологического факторов привело к возникновению многочисленных элементов тектонического и литологического экранирования.
Общие сведения об алгоритме
Дифференциальная эволюция (DE) – это параллельный метод прямого поиска, который использует некоторые особенности эволюционных алгоритмов (ЭА). Другими словами, DE – это метод, который оптимизирует проблему путем итеративного улучшения решений-кандидатов с учетом заданной меры качества [5].
Алгоритм DE имеет популяцию решений-кандидатов, которые называются агентами. Компоненты каждого агента в N-мерном пространстве составляют переменные решения задачи оптимизации. Эти агенты перемещаются в пространстве решений с помощью операторов кроссинговера и мутации, которые объединяют и изменяют их позиции. Другими словами, пробные агенты создаются на основе старых агентов, затем проверяется, «выбьет» ли он самого слабого текущего агента. Однако дифференциальная эволюция создает по одному новому кандидату (или «пробному вектору») для каждого существующего члена («вектора-кандидата») популяции, поэтому существует несколько потенциальных новых решений. В этом отношении DE напоминает советников, поскольку в нем применяются генетические операторы для получения новых решений. Выбор решений осуществляется на основе «жадных критериев». Если новая позиция агента является улучшенной, она принимается и заменяет старое решение. Улучшенный пробный агент называется успешным и добавляется в популяцию решений. В противном случае пробный агент считается неудачей, и он отбрасывается из прямого поиска. В таблице 1 перечислены характеристики DE [6, 7].
Таблица 1. Сравнение характеристик алгоритмов
|
Общий алгоритм |
Дифференциальная эволюция |
|
Переменная решения Решение Старое решение Новое решение Лучшее решение Фитнес-функция Начальное решение Выбор Процесс генерации нового решения |
Координата положения агента Агент (позиция) Старый агент Пробный агент – Желательность агента Случайный агент Жадный критерий Мутация и кроссинговер |
Пробное решение Xj (новое) сравнивается со старым решением Xj, чтобы определить, становится ли оно членом популяции решений. Если пробное решение имеет лучшее значение пригодности, чем старое решение, оно заменяет его. В противном случае пробное решение удаляется, а старое решение сохраняется в популяции. Этот процесс выбора называется жадным критерием.
DE начинается со случайной генерации множества решений – начальной популяции агентов. Для каждого агента (решения) генерируется новое пробное решение или агент. Для генерации пробного агента требуется, чтобы 3 агента из старой популяции были выбраны случайным образом, а новое решение генерируется с помощью эвристической функции. Этот процесс известен как мутация. Оператор кроссинговера применяется для объединения старого агента и нового сгенерированного решения [8, 11].
В результате получается пробное решение. Пробное решение заменяет старое решение, если оно имеет лучшее значение пригодности в соответствии с критериями жадности. В противном случае старое решение остается в популяции. Пробные решения снова подбираются, если критерии завершения не удовлетворены. В противном случае сообщается окончательная версия решений и алгоритм завершается. На рисунке 3 показана блок-схема алгоритма DE [9, 12].
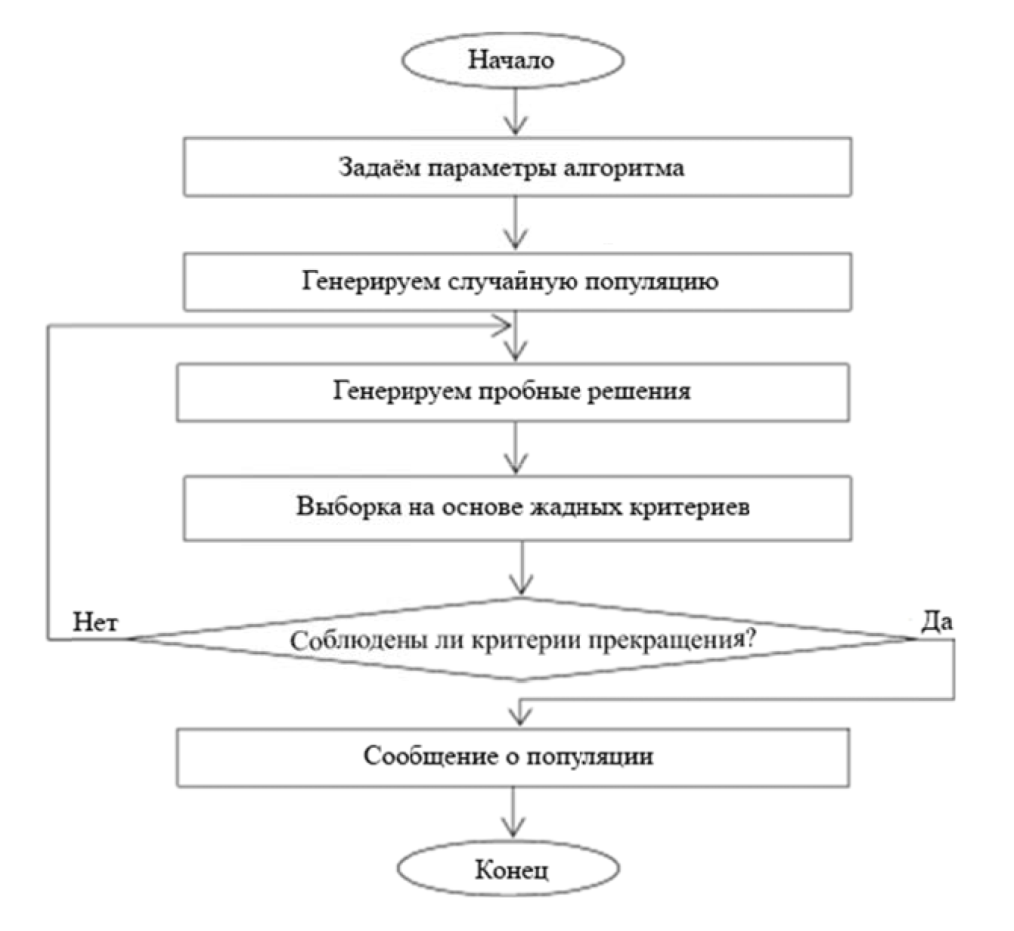
Размер популяции M, коэффициент мутации d, константа кроссинговера C и критерии завершения – это параметры DE, определяемые пользователем. Хороший выбор параметров зависит от пространства решений конкретной задачи, и оптимальное значение параметров для одной проблемы имеет ограниченную полезность для других проблем. Следовательно, определение оптимального значения параметров часто требует выполнения большого числа вычислительных экспериментов. Разумным методом поиска подходящих значений параметров является проведение анализа чувствительности, при котором тестируются комбинации параметров и алгоритм запускается несколько раз для каждой комбинации, чтобы учесть случайный характер алгоритма решения.
Таким образом, аналитик получает распределение решений и соответствующих значений объективной функции для каждой комбинации параметров. Сравнение результатов всех комбинаций параметров дает рекомендации по правильному выбору параметров алгоритма.
Создание начальной популяции
Каждое возможное решение задачи оптимизации, найденное с помощью DE, называется агентом. В N-мерной проблеме оптимизации компонент агента в любом измерении N-мерного пространства является переменной решения оптимизационной задачи. Агент – это массив размером 1 ´ N [10, 13]:
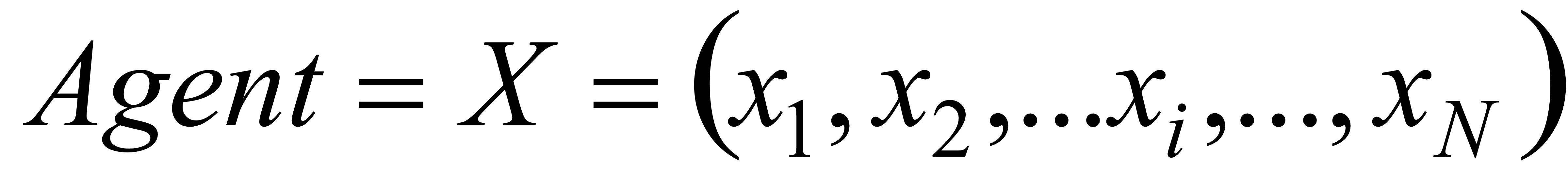 ,
,
где X – возможное или предварительное решение задачи оптимизации; xi = ith – переменная решения X; N – количество переменных решения. Для запуска алгоритма оптимизации матрица агентов размером M x N генерируется случайным образом, где M и N – размер популяции и количество переменных решения соответственно. Эта матрица представлена следующим образом:
 ,
,
где Xj – j-е решение; Xj,i = ith – переменная решения j-го решения; M – размер популяции.
Каждое из значений переменной решения j-го решения (Xj,1, Xj,2, Xj,3, … , Xj,N) представляется в виде числа с плавающей точкой (вещественные значения). Алгоритм DE решает задачи с непрерывным пространством решений.
DE генерирует новые пробные решения с помощью операций мутации и кроссинговера, действуя последовательно. Новое пробное решение Xj сначала генерируется путем мутации. Оператор кроссинговера применяется к вновь сгенерированному решению, которое объединяет старое решение и вновь сгенерированное решение для получения пробного решения Xj (новое). Этот процесс выполняется для каждого члена популяции решений.
Мутация
На рисунке 4 показан шаг «мутации». x1 и x2 – это оси пространства решений, т. е. место, где мы будем искать оптимальное решение для некоторой объективной функции. Итак, Xi = (xi1, xi2), называемый вектором-кандидатом, представляет собой решение, которое в настоящее время существует в популяции, в каждом поколении существует NP таких решений. Мы оставили Xi в левой части диаграммы для ясности. Xr0, Xr1 и Xr2 – случайно выбранные различные члены популяции; d – вектор, соединяющий Xr1 и Xr2, который умножается на масштабный коэффициент F и прибавляется к Xr0. Результат называется вектором мутанта V, а Xr0 называется родительским вектором. F обычно принимает значение от 0 до 2.
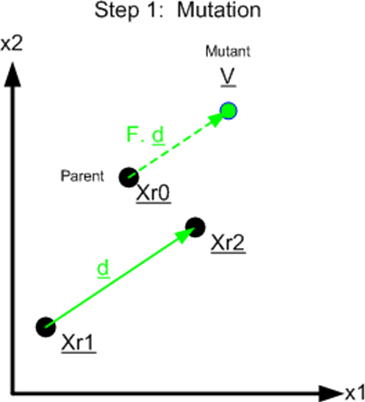
Рисунок 4. Генерация решения методом мутации
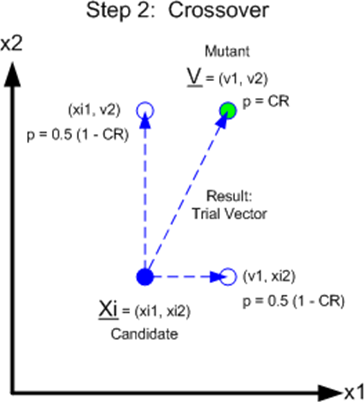
Рисунок 5. Генерация решения методом кроссинговера
Кроссинговер
Рисунок 5 иллюстрирует этап «кроссинговера», на котором мутантный вектор и вектор-кандидат «скрещиваются», чтобы увидеть, получится ли в результате подходящий «ребенок». Новый кандидат называется пробным вектором. Алгоритм устанавливает значения элементов пробного вектора путем случайного выбора соответствующего элемента из мутанта или кандидата. Вероятность выбора элемента из мутанта равна CR «скорости кроссинговера». Очевидно, что существует конечная вероятность того, что ни один из элементов мутантного вектора не будет выбран: (1 – CR)^2 в двумерном случае. Чтобы избежать этого, алгоритм случайным образом выбирает элемент из {1, 2} с равномерной вероятностью, и этот элемент берется из мутантного вектора. Это означает, что пробный вектор никогда не будет равен вектору-кандидату. Пробный вектор равен мутантному вектору с вероятностью CR (потому что хотя бы 1 элемент изменится с вероятностью 1). Две другие возможности для пробного вектора (движение по оси x1 или движение по оси x2) происходят с вероятностями 0,5(1 – CR) [14, 15].
Псевдокод дифференциальной эволюции
Ниже (рис. 6) представлен псевдокод для примерного понимания, как работает алгоритм на рисунках 4 и 5.

Рисунок 6. Псевдокод дифференциальной эволюции
Создание оптимальной траектории скважины
Для реализации проекта по внедрению оптимальной горизонтальной скважины в модель пласта воспользуемся специализированным ПО – tNavigator 2021 года. После выбора необходимого участка месторождения, на котором планируется установка горизонтальной скважины, создается геологическая модель пласта, достаточная для прогнозирования, и устанавливаются двойники реальных скважин.
Следуя инструкции, создаем файл BaseModel.data.
Чтобы начать работу с проектом, нам понадобится базовая гидродинамическая модель (нефтенасыщенный пласт) в формате Е1 (рис. 7), которая импортируется в дизайнер моделей.
При помощи workflow нужно добавить 2 скважины со статической геометрией и 1 с вариативной геометрией. Геометрические параметры этой скважины будут использованы в качестве переменных при осуществлении процесса оптимизации.
В модели есть две добывающие скважины w1 и w2 и участок, в который мы предварительно добавим новую горизонтальную скважину w3 (рис. 8). Она не должна выходить за пределы модели.

Рисунок 7. Стандартная гидродинамическая модель
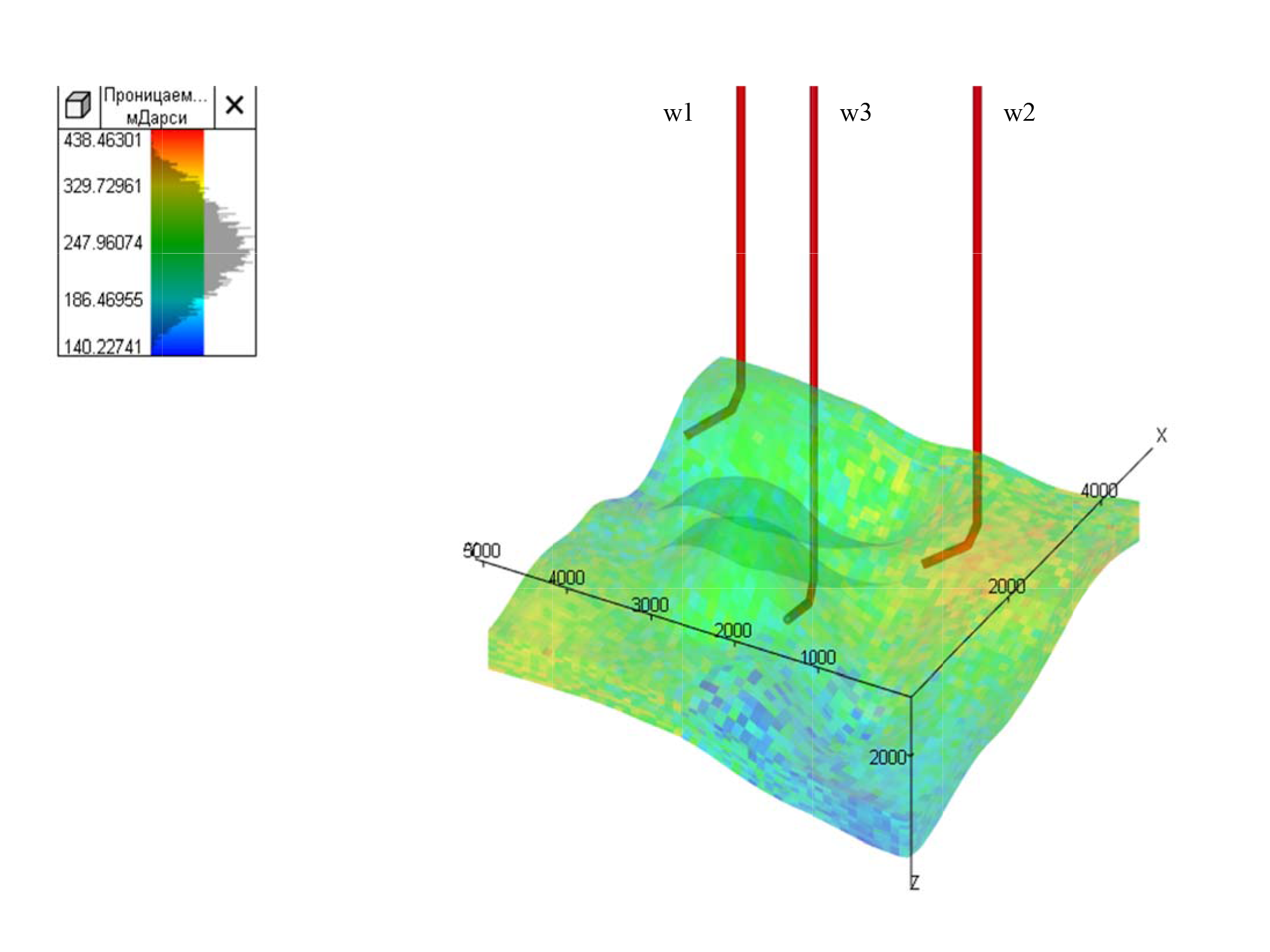
Рисунок 8. Базовая гидродинамическая модель
Начальные параметры скважины задаются в окне «Расчеты» и Workflow или импортируются в том же рабочем окне. Выставляем начальные положения для модели (таб. 2).
Таблица 2. Начальные координаты скважины w3
|
|
Начальное значение |
Минимальное значение |
Максимальное значение |
|
X |
2500 |
100 |
4900 |
|
Y |
2500 |
100 |
4900 |
|
ALPHA |
180 |
0 |
360 |
|
BETA |
0 |
– 90 |
90 |
Х, Y – 2D-координаты точки Т1;
ALPHA (a) – азимут первого горизонтального участка скважины (T1 – T2);
BETA (b) – отклонение от ALPHA второго горизонтального участка скважины (T2 – T3).
На рисунке 9 представлен подбор оптимального (центрального) расположения траекторий скважины для получения наибольшего извлечения продукции.
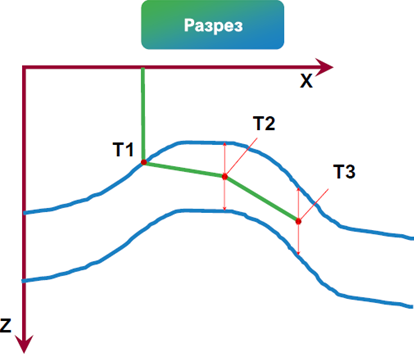 |
Рисунок 9. Траектория расположения горизонтальных участков скважины
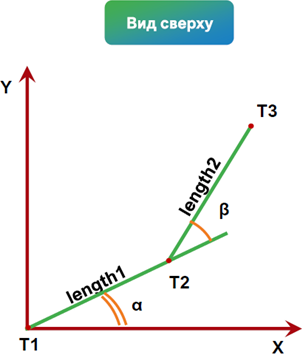
Рисунок 10. Углы наклона разных участков скважины
Длины горизонтальных участков – length1 (длина T1 – T2) и length2 (длина T2 – T3) постоянны. В случае надобности они тоже могут быть заданы как переменные либо их количество может быть увеличено при необходимости с задачей дополнительных точек (T4 – Tn) в зависимости от поставленной задачи. Угол поворота скважины также подбирается автономно (рис. 10).
Для удержания скважины внутри продуктивного интервала нужно задать горизонты. Горизонт Top создан при помощи расчета «Создать горизонт Кровли/Подошвы по сетке». Для добавления этого расчета в Workflow: Структурное моделирование ➝ Горизонт ➝ Создать горизонт Кровли/Подошвы по сетке. Горизонт представляет собой верх сетки и имеет одинаковые с сеткой горизонтальные размеры. Подошва добавляется тем же способом. Ставим галочку «Учитывать пустые узлы» и ставим данные из таблицы 3 и «Автоопределение».
Таблица 3. Ограничения условий оптимизации
|
Результирующий горизонт |
Top |
|
Сетка |
BaseModel |
|
Тип залегания |
Кровля |
|
Свойства сетки |
|
|
Угол, градусы |
0 |
|
Минимальное значение Х, м |
0 |
|
Длина по Х, м |
5000 |
|
Шаг по Х, м |
100 |
|
Минимальное значение Y, м |
0 |
|
Длина по Y, м |
5000 |
|
Шаг по Y, м |
100 |
|
Автоопределение позиции |
Скважины |
|
Отступы по XY, м |
0 |
Следующим шагом через функцию «Добавить код вручную» в командном окне Workflow добавляем в программу код, написанный на языке программирования Python, который работает следующим образом.
Начальная точка новой скважины описывается координатами (X, Y), где X и Y – переменные в процессе оптимизации.
Координата Z точки T1 – это кровля горизонта.
2D-координаты точек T2 и T3 рассчитываются при помощи ALPHA и BETA.
Если сегмент скважины не вмещается в сетку, он укорачивается до тех пор, пока не начинает вмещаться.
То же самое повторяется для точки T3.
Координаты Z точек T2 и T3 находятся посередине между горизонтами Top и Bottom на заданных 2D-координатах.
Новая скважина создается при помощи функции wells_create.
Перфорации для новой скважины помещаются в таблицу структуры скважин функциями add_record() и set_value().
Чтобы задать перфорацию скважины на глубине и очередность перфорации, нам потребуется функция «Ввод конструкции скважин», которая добавляет в секцию SCHEDULE (секция используется для задания значений добычи и закачки для всей модели, продолжения моделирования и задания других данных, зависящих от времени). Ключевые слова COMPDATMD (задание перфораций по глубине) и COMPORD (задание очередности перфорации).
Для добавления этой опции в workflow следует зайти в Данные по скважинам ➝ Глобальные правила ➝ Ввод конструкции скважин. Мы используем ее для добавления параметров в скважину w3.
Для контролирования параметров скважины (в нашем случае w3) мы обращаемся к функции «Управление добывающими скважинами (прогноз)». Для добавления этой опции в workflow следует зайти: Данные по скважинам ➝ Правила на шагах ➝ Скважины ➝ Управление.
Устанавливаем режим контроля – BHP (50 Бар), ограничение добычи жидкости 1000 ст. м3/сут. Значения могут меняться в зависимости от начальных условий.
После выставления нужных нам начальных параметров и установки кода можно приступать к моделированию новых условий.
Нажимаем «Запустить Workflow». Корректно выполненные процедуры подсветятся зеленым цветом. При включении отображения прозрачной сетки скважины должна появиться обновленная модель с новой скважиной w3 (рис.11).
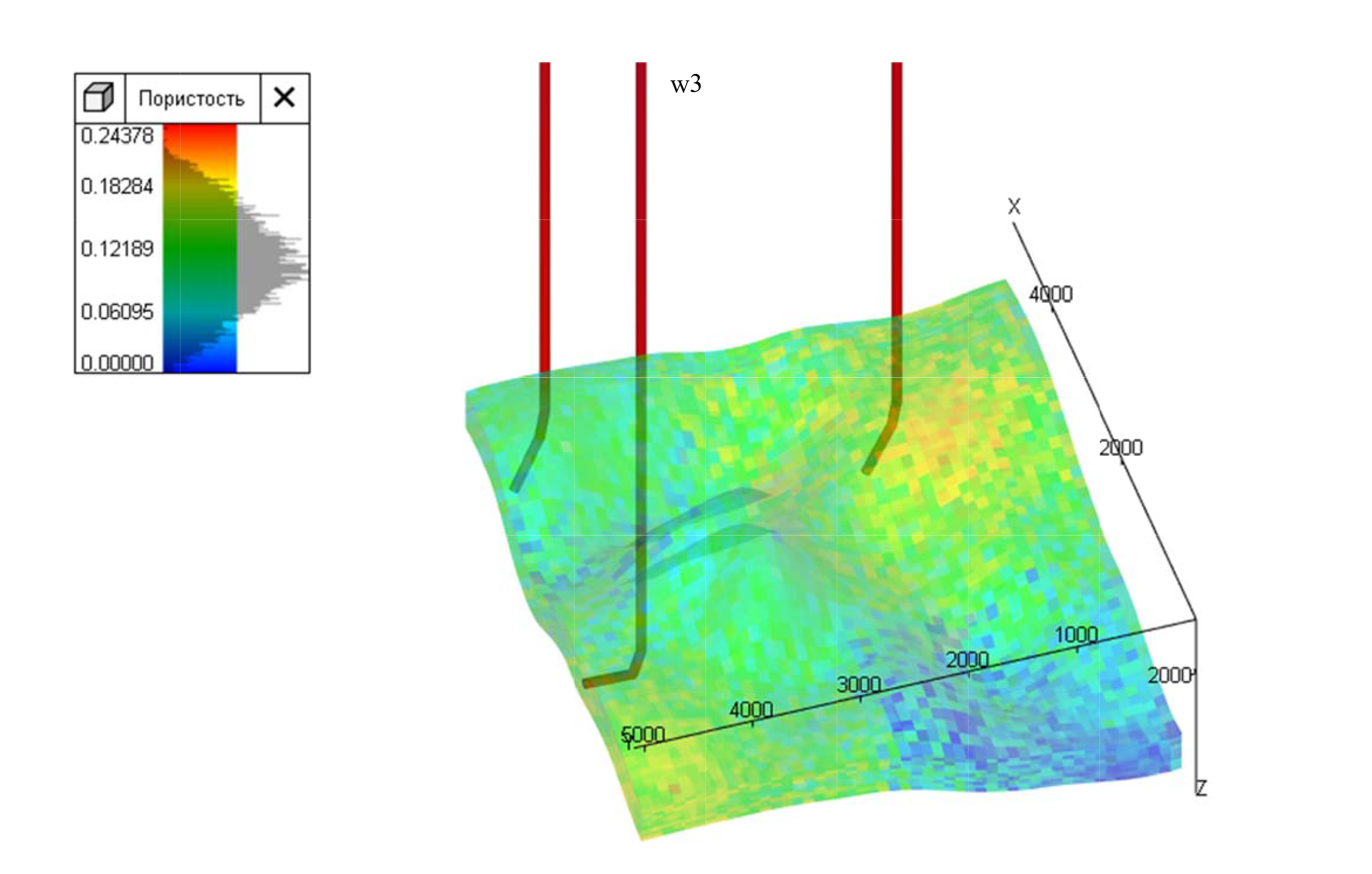
Рисунок 11. Отображение новой скважины w3
Для инициализации динамической модели нажимаем зеленую кнопку и создаем проект адаптации модели, используя текущую динамическую модель с последующим сохранением проекта. Далее создаем проект адаптации модели, используя текущую динамическую модель. Нажимаем желтую кнопку. Происходит вычисление модели.
Для создания целевой функции вводим имя проекта, которое называется OF1. Выключаем «Запустить анализ чувствительности» и «Запустить оптимизацию адаптации», нажимаем «OK» – появляется окно нового AHM проекта «Создать новый эксперимент». Выбираем тип алгоритма «Дифференциальная эволюция», нажимаем «Выбрать целевую функцию» – в появившемся окне нажимаем «Конфигурировать». В открывшемся окне задаем параметры функции (таб. 4). Тип функции – «Оптимизация на прогнозе».
Таблица 4. Параметры оптимизации
|
Тип объекта |
Параметр |
Режим |
|
месторождение |
накопленная нефть |
максимизация накопленной добычи |
|
месторождение |
накопленная вода |
минимизация накопленной добычи |
Остальные данные оставляем неизменными. Нажимаем «Создать эксперимент …», чтобы вернуться в окно «Создать новый эксперимент». Выбираем тип «Дифференциальная эволюция» и все переменные: ALPHA, BETA, X, Y. Выбираем «Глобальный поиск» (для поиска глобального оптимума). Нажимаем «Выбрать целевую функцию» и выбираем только что созданную функцию OF1. Для запуска расчетов нажимаем «OK».
Через некоторое время останавливаем расчет. Нажимаем вкладку «Результаты > Таблица». Рассматриваем варианты конфигурации по нашей целевой функции OF1. Чем выше значение, тем лучше вариант конфигурации скважины (выше накопленные значения нефти и ниже воды), (таб. 5). Отсортируем по колонке OF1, нажав на ее заголовок:
OF1 = – ½ × (накопленная вода – накопленная нефть).
Таблица 5. Результаты прогнозирования
|
Модели |
OF1 |
ALPHA |
BETA |
X |
Y |
Среднее давление, бар |
Дебит нефти ст. м3/сут. |
Дебит воды ст. м3/сут. |
|
.00070 |
473082 |
117 |
– 23 |
1724 |
4443 |
190 |
2534 |
466 |
|
.00028 |
473023 |
0 |
49 |
1545 |
4704 |
190 |
2534 |
466 |
|
.00072 |
473015 |
45 |
67 |
757 |
4900 |
189 |
2535 |
465 |
|
.00049 |
473006 |
359 |
41 |
1355 |
4900 |
189 |
2534 |
466 |
|
.00042 |
472983 |
256 |
– 41 |
1228 |
4900 |
189 |
2534 |
466 |
|
.00025 |
472963 |
158 |
– 22 |
1549 |
4678 |
190 |
2534 |
466 |
|
.00048 |
472962 |
319 |
8 |
1228 |
4900 |
190 |
2532 |
468 |
|
.00040 |
472961 |
201 |
– 12 |
1106 |
4900 |
189 |
2535 |
465 |
|
.00080 |
472902 |
210 |
50 |
1837 |
4443 |
191 |
2534 |
466 |
|
.00017 |
472888 |
306 |
– 4 |
488 |
4900 |
189 |
2533 |
467 |
|
.00001 |
472863 |
310 |
52 |
865 |
4900 |
189 |
2534 |
466 |
|
.00078 |
472849 |
211 |
– 18 |
2270 |
4443 |
191 |
2534 |
466 |
|
.00063 |
471771 |
144 |
– 47 |
577 |
4900 |
189 |
2517 |
483 |
|
.00073 |
470105 |
77 |
– 42 |
1898 |
4209 |
191 |
2462 |
538 |
|
.00053 |
465008 |
190 |
– 22 |
451 |
4900 |
189 |
2497 |
503 |
|
.00052 |
464413 |
183 |
8 |
565 |
4900 |
189 |
2492 |
508 |
|
.00056 |
462564 |
0 |
10 |
2268 |
3693 |
193 |
2414 |
586 |
|
.00059 |
462288 |
263 |
– 24 |
599 |
4900 |
189 |
2447 |
553 |
|
.00021 |
459718 |
130 |
46 |
488 |
4900 |
189 |
2474 |
526 |
|
.00035 |
455954 |
266 |
21 |
252 |
4900 |
190 |
2421 |
579 |
|
.00046 |
445357 |
116 |
28 |
100 |
4796 |
189 |
2415 |
568 |
|
.00079 |
440641 |
23 |
– 19 |
4900 |
1181 |
190 |
2366 |
634 |
|
.00038 |
437729 |
0 |
– 16 |
4605 |
1128 |
190 |
2352 |
648 |
|
.00039 |
437422 |
319 |
– 16 |
4900 |
686 |
189 |
2346 |
654 |
|
.00060 |
433873 |
61 |
8 |
2669 |
2659 |
194 |
2270 |
730 |
|
.00066 |
431736 |
254 |
– 90 |
2566 |
4524 |
192 |
2257 |
743 |
|
.00008 |
428082 |
182 |
– 6 |
4031 |
982 |
192 |
2245 |
755 |
|
.00071 |
419719 |
236 |
– 22 |
2487 |
4900 |
192 |
2199 |
801 |
|
.00004 |
416080 |
142 |
– 25 |
4208 |
745 |
191 |
2246 |
754 |
|
.00065 |
398932 |
56 |
54 |
100 |
4047 |
190 |
2259 |
741 |
|
.00036 |
395419 |
172 |
– 32 |
2421 |
4900 |
193 |
2060 |
940 |
|
.00068 |
394353 |
182 |
– 64 |
4823 |
4900 |
193 |
1965 |
1035 |
|
.00067 |
389478 |
56 |
55 |
100 |
4004 |
191 |
2248 |
752 |
|
.00037 |
385049 |
295 |
– 44 |
591 |
4263 |
192 |
2186 |
814 |
|
.00044 |
381263 |
266 |
0 |
100 |
4422 |
191 |
2217 |
783 |
|
.00082 |
352486 |
245 |
– 48 |
1671 |
3964 |
193 |
2063 |
937 |
|
.00075 |
351969 |
32 |
– 19 |
1455 |
3372 |
194 |
2013 |
987 |
|
.00027 |
327104 |
0 |
– 30 |
4605 |
2005 |
194 |
1889 |
1111 |
|
.00014 |
312970 |
306 |
– 5 |
3099 |
1122 |
194 |
1903 |
1097 |
|
.00013 |
312866 |
306 |
– 2 |
100 |
3827 |
193 |
1934 |
1066 |
|
.00023 |
280178 |
21 |
– 20 |
3306 |
1288 |
194 |
1725 |
1275 |
|
.00050 |
277201 |
115 |
– 18 |
515 |
2318 |
195 |
1810 |
1190 |
|
.00055 |
264596 |
59 |
– 37 |
4371 |
3544 |
195 |
1699 |
1301 |
|
.00081 |
256389 |
0 |
– 19 |
4157 |
3964 |
195 |
1599 |
1401 |
|
.00016 |
251041 |
306 |
– 67 |
488 |
3012 |
195 |
1771 |
1229 |
|
.00020 |
249381 |
0 |
– 6 |
2469 |
4404 |
194 |
1829 |
1171 |
|
.00084 |
246868 |
263 |
– 19 |
3242 |
3493 |
195 |
1777 |
1223 |
|
.00077 |
212320 |
197 |
– 12 |
3242 |
3964 |
195 |
1741 |
1259 |
|
.00000 |
211601 |
180 |
0 |
2500 |
2500 |
195 |
1666 |
1334 |
|
.00003 |
211123 |
158 |
79 |
922 |
3676 |
194 |
1659 |
1341 |
|
.00010 |
188702 |
95 |
– 68 |
2818 |
4100 |
195 |
1685 |
1315 |
|
.00015 |
188662 |
291 |
– 5 |
100 |
2930 |
195 |
1650 |
1350 |
|
.00031 |
185850 |
293 |
16 |
518 |
2976 |
195 |
1642 |
1358 |
|
.00009 |
184301 |
245 |
– 19 |
3242 |
3964 |
195 |
1670 |
1330 |
|
.00045 |
181110 |
319 |
29 |
2771 |
4249 |
195 |
1697 |
1303 |
|
.00074 |
179696 |
196 |
– 64 |
1971 |
2519 |
195 |
1640 |
1360 |
|
.00069 |
173909 |
23 |
5 |
445 |
2519 |
195 |
1659 |
1341 |
|
.00083 |
173660 |
207 |
– 90 |
3242 |
3962 |
195 |
1612 |
1388 |
|
.00057 |
162528 |
102 |
– 40 |
1355 |
2643 |
195 |
1613 |
1387 |
|
.00085 |
152241 |
84 |
– 44 |
3196 |
2931 |
195 |
1624 |
1376 |
|
.00047 |
150957 |
0 |
14 |
783 |
3270 |
195 |
1597 |
1403 |
|
.00029 |
150482 |
56 |
– 5 |
1027 |
3069 |
195 |
1607 |
1393 |
|
.00012 |
149932 |
355 |
– 5 |
406 |
2839 |
195 |
1617 |
1383 |
|
.00041 |
149573 |
179 |
– 16 |
3361 |
4647 |
195 |
1613 |
1387 |
|
.00007 |
146421 |
236 |
– 64 |
4823 |
2519 |
195 |
1617 |
1383 |
|
.00005 |
139563 |
359 |
– 22 |
1355 |
2318 |
195 |
1597 |
1403 |
|
.00006 |
137747 |
319 |
– 16 |
1228 |
3270 |
195 |
1577 |
1423 |
|
.00002 |
136999 |
293 |
– 22 |
4264 |
2309 |
195 |
1576 |
1424 |
|
.00086 |
133087 |
269 |
12 |
3242 |
3964 |
195 |
1566 |
1434 |
|
.00043 |
132425 |
319 |
– 19 |
3283 |
3270 |
195 |
1581 |
1419 |
|
.00076 |
132280 |
357 |
– 28 |
3242 |
4574 |
195 |
1566 |
1434 |
|
.00024 |
129142 |
0 |
– 22 |
1657 |
2309 |
195 |
1573 |
1427 |
|
.00058 |
127055 |
359 |
– 88 |
4102 |
2382 |
195 |
1557 |
1443 |
|
.00032 |
126463 |
53 |
– 22 |
3463 |
2309 |
195 |
1562 |
1438 |
|
.00022 |
125828 |
313 |
– 8 |
100 |
2439 |
195 |
1555 |
1445 |
|
.00033 |
125762 |
293 |
– 65 |
1355 |
2309 |
195 |
1579 |
1421 |
|
.00064 |
116447 |
236 |
53 |
100 |
2519 |
195 |
1547 |
1453 |
|
.00051 |
112274 |
0 |
– 22 |
3360 |
3546 |
195 |
1542 |
1458 |
|
.00062 |
112025 |
32 |
– 28 |
2512 |
1814 |
195 |
1551 |
1449 |
|
.00034 |
111704 |
0 |
– 29 |
3915 |
2587 |
195 |
1550 |
1450 |
|
.00061 |
110315 |
0 |
– 12 |
3675 |
3487 |
195 |
1541 |
1459 |
|
.00026 |
110263 |
142 |
– 22 |
4264 |
2309 |
195 |
1541 |
1459 |
|
.00030 |
108142 |
182 |
– 90 |
3956 |
2309 |
195 |
1537 |
1463 |
|
.00019 |
107618 |
0 |
– 9 |
3648 |
3128 |
195 |
1538 |
1462 |
|
.00011 |
107286 |
306 |
– 5 |
488 |
1288 |
195 |
1534 |
1466 |
|
.00018 |
107069 |
172 |
– 19 |
1212 |
1288 |
195 |
1534 |
1466 |
|
.00054 |
106930 |
0 |
– 22 |
1355 |
760 |
195 |
1533 |
1467 |
Желтым цветом обозначены отсортированные расположения базовой скважины и наилучшей, которую сгенерировал алгоритм. После выбора расположения скважины нужно, чтобы tNavigator построил модель этой скважины для наглядности.
Правой кнопкой мыши нажимаем на лучший вариант и выбираем «Установить значения переменных этого варианта в Workflow». В дизайнере моделей должно будет произойти изменение – скважина сместится на новые координаты. В нашем случае скважина уже смоделирована оптимальным образом по имеющимся данным прогноза (рис. 11).
При проведении большего количества прогнозов можно добиться еще лучшего результата. Данный вариант имеет самые высокие показатели нефтеизвлечения среди 86 результатов прогнозирования (таб. 6).
Таблица 6. Координаты наилучшей скважины
|
|
Начальное значение |
Минимальное значение |
Максимальное значение |
|
X |
1724 |
100 |
4900 |
|
Y |
4443 |
100 |
4900 |
|
ALPHA |
117 |
0 |
360 |
|
BETA |
– 23 |
– 90 |
90 |
На рисунке 12 приведен программный код.


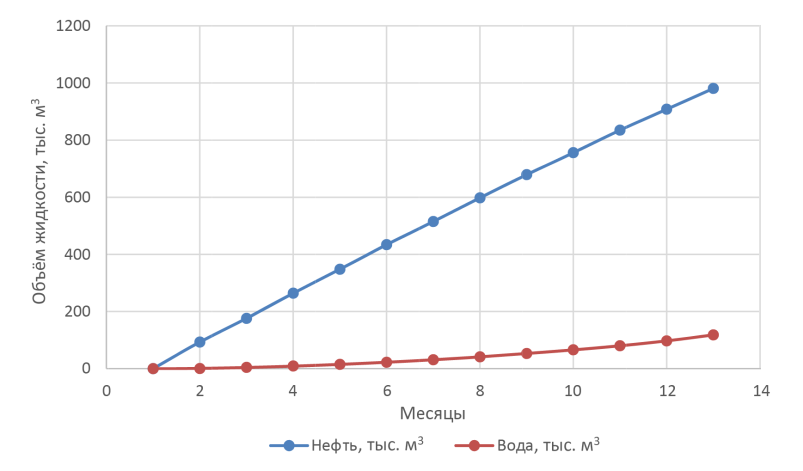
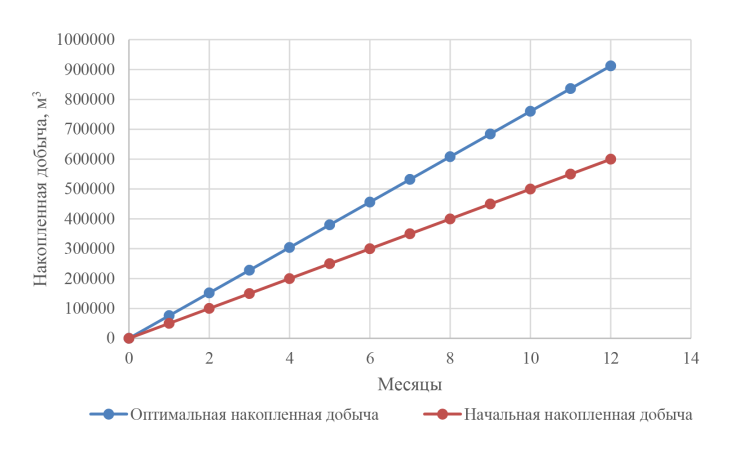
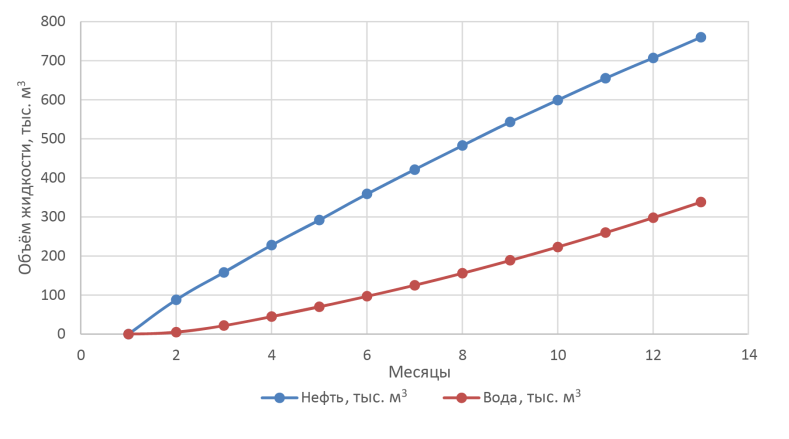
На рисунке 13 приведено сравнение накопленной добычи нефти двух вариантов, на рисунках 14 и 15 – накопленная добыча жидкости базового и оптимизированного варианта.
 |
 |
|
|
|
||
|
Рисунок 15. Накопленная добыча жидкости оптимизированного варианта |
|
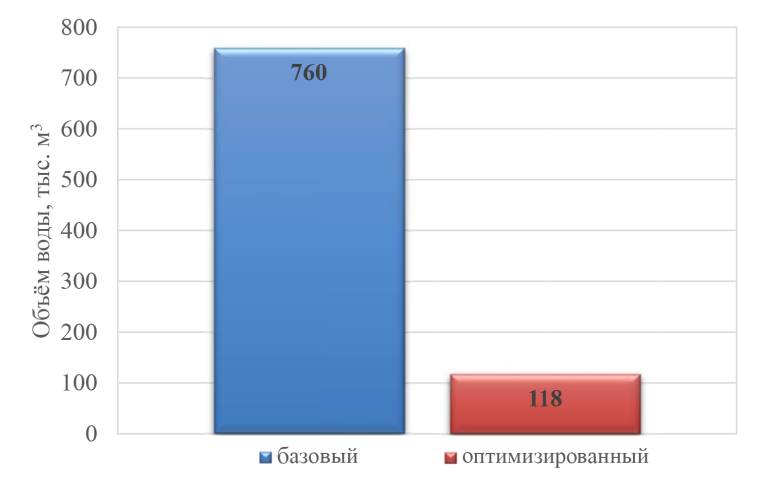
На рисунках 16 и 17 приведены гистограммы с результирующими показателями накопленной добычи нефти и воды для двух вариантов.
 |
|
Заключение
Целью данной работы являлась оптимизация проектной базовой траектории скважины, т. е. подбор новой, более совершенной траектории для увеличения нефтедобычи и уменьшения извлечения воды с помощью моделирования участка пласта с внедрением в него алгоритма дифференциальной эволюции.
Эксперименты показали, что данный метод оптимизации траектории скважин отлично справляется с поставленными задачами и экономически более целесообразен по сравнению со стандартными методами расчета.
Данный метод оптимизации траектории бурения скважины является перспективным и эффективным методом увеличения нефтеотдачи и уменьшения извлечения воды; он позволит уменьшить количество эксплуатационных расходов за счет сокращения штата сотрудников, проведения прогнозной аналитики, комплексной оптимизации уровня активов, а также позволит уменьшить время на реализацию проекта.
1. Брызгунов Р. П. Ускорение сроков строительства скважины на Чаяндинском нефтегазоконденсатном месторождении / Брызгунов Р. П., Савенок О. В. // Рассохинские чтения: материалы международной конференции (4–5 февраля 2021 года, г. Ухта): в 3 частях. – Ухта: Ухтинский государственный технический университет, 2021. – С. 152–158.
2. Рыжов А. Е. Определение степени влияния тектонического фактора на формирование залежей углеводородов на Саманчакитском блоке Чаяндинского нефтегазоконденсатного месторождения / Рыжов А. Е., Крикунов А. И., Филиппова Л. А., Канунникова Н. Ю., Саприна О. А. // Вести газовой науки (научно-технический сборник). – 2014. – № 3 (19). – С. 99–105.
3. Севостьянова Р. Ф. Хамакинский горизонт Чаяндинского месторождения в свете новых геологических и поисково-разведочных данных / Севостьянова Р. Ф. // Нефтегазовая геология. Теория и практика. – 2017. – Т. 12. – № 1. – DOI:https://doi.org/10.17353/2070-5379/3_2017. – URL: http://www.ngtp.ru/rub/4/3_2017.pdf.
4. Токарев Д. А. Осинская подсвита усольской свиты нижнего кембрия центральной и южной частей Непско-Ботуобинской антеклизы: строение, условия формирования и биостратиграфическая характеристика / Токарев Д. А., Плюснин А. В., Терлеев А. А., Староселец Д. А., Никулин Е. В., Афонин И. В., Агашева Е. А. // Известия Томского политехнического университета. Инжиниринг георесурсов. – 2024. – Т. 335. – № 3. – С. 176–191. – DOI:https://doi.org/10.18799/24131830/2024/3/4275
5. Gong W. An efficient multi‐objective differential evolution algorithm for engineering design / Gong W., Cai Z. and Zhu L. // Structural and Multidisciplinary Optimization. – 2009. – № 4 (2). – С. 137–157.
6. Hooke R. Direct search solution of numerical and statistical problems / Hooke R., Jeeves T.A. // Journal of the ACM. – 1961. – № 8 (2). – С. 212–229.
7. Lakshminarasimman L. Applications of differential evolution in power system optimization / Lakshminarasimman L., Subramanian S. // Advances in differential evolution, Studies in computational intelligence. – Берлин: Springer, 2008. – Т. 143. – C. 257–273.
8. Price K. V. Differential evolution: A practical approach to global optimization / Price K. V., Storn R. M., Lampinen J. A. – Springer Nature Link, 2005.
9. Storn R. Differential evolution – a simple and efficient heuristic for global optimization over continuous spaces / Storn R., Price K. // Journal of Global Optimization. – 1997. – № 11 (4). – С. 341–359.
10. Gonuguntla V. Differential evolution with population and strategy parameter adaptation / Gonuguntla V., Mallipeddi R., Veluvolu K. C. // Mathematical Problems in Engineering. – 2015. – С. 287607.
11. Арутюнян А.С. Drill cuttings control system in oil and gas companies / Арутюнян А. С., Петрушин Е.О., Кусов Г. В., Кусова Л. Г. // IOP Conference Series: Earth and Environmental Science. – 2021. – С. 012077. – DOI:https://doi.org/10.1088/1755-1315/720/1/012077.
12. Lampinen J. Mechanical engineering design optimization by differential evolution / Lampinen J., Zelinka I. // New ideas in optimization. – Maidenhead: McGraw Hill, 1999. – С. 127–146.
13. Alrazzaq A. Development of East Baghdad Oil Field By Clusters of Horizontal Wells / Alrazzaq A., Alhaleem A. A. // Journal of Chemical and Petroleum Engineering. – 2019. – № 10. – DOI: https://doi.org/10.31699/IJCPE.2019.3.10.
14. Daiwen Xu. Application of branch horizontal well technology in HFY Oilfield of Iraq / Daiwen Xu, Mei Jingbin, Zheng Chuankui, Ren Zhiji, Zou Ke // Oil Drilling & Production Technology. – 2014.
15. Hamada G. M. Contribution of horizontal drilling technology in the development programs of Saudi oil fields / Hamada G. M., AI-Awad M. N. J., AI-Biehed M. S., AI-Saddique M. A. // Engineering Journal of the University of Qatar. – 2001.