Повышение разрешающей способности вибросейсмического сигнала за счет использования гармоник

Денисов Михаил Сергеевич; Зыков Андрей Александрович

doi:doi:

Главная / Журналы / Вестник АГГИ / Номер 4 / Повышение разрешающей способности вибросейсмического сигнала за счет использования гармоник

Отправить рукопись Скачать PDF
Текст

Цитировать

Цитирований:

Повышение разрешающей способности вибросейсмического сигнала за счет использования гармоник

Журнал: ВЕСТНИК АГГИ № 4 , 2025

Рубрики: ГЕОЛОГИЯ И ГЕОЛОГО-РАЗВЕДОЧНЫЕ РАБОТЫ

Денисов Михаил Сергеевич ¹

Зыков Андрей Александрович ²

Информация об авторах и публикации

Авторы:

1. ООО ГЕОЛАБ (директор по науке)
сотрудник с 01.01.2006 по 01.01.2025

ООО ГЕОЛАБ (директор по науке)

ООО ГЕОЛАБ (директор по науке)
с 01.01.2006 по 01.01.2025
Россия

2. ООО ГЕОЛАБ (геофизик)
сотрудник с 01.01.2020 по 01.01.2025

г. Москва и Московская область, Россия

Тип:

Статья

Страницы:

с 36 по 46

Статус:

В работе

Получено:

03.02.2025

Одобрено:

19.03.2025

Опубликовано:

25.03.2025

Классификаторы:

ВАК 1.6 Науки о Земле и окружающей среде
ВАК 1.2.1 Искусственный интеллект и машинное обучение
ВАК 1.2.2 Математическое моделирование, численные методы и комплексы программ
УДК 550.834 Использование упругих волн для изучения верхней части разреза. Сейсмический и акустический методы поисков, разведки и зондирования

Язык материала:

русский

Ключевые слова:

вибрационная сейсморазведка, сигнал, спектр, гармоники.

Аннотация и ключевые слова

Аннотация (русский):
В вибрационной сейсморазведке регистрируются так называемые кратные частоты, также известные как гармоники. Их интенсивность зависит и от условий контакта вибрационной плиты с грунтом, и от конструкции самой вибрационной установки. Обычно они рассматриваются как помеха, подлежащая устранению. Однако гармоники, наряду с основным сигналом, проходят в глубь среды, где, как и основной сигнал, взаимодействуют с целевыми границами. Таким образом, они несут в себе информацию о глубинном строении земной коры. Гармоники характеризуются более широким, чем у основного сигнала, частотным диапазоном, поэтому они могут быть использованы для повышения разрешенности сейсмической записи.

Ключевые слова:
вибрационная сейсморазведка, сигнал, спектр, гармоники.

Текст

Текст (PDF): Читать Скачать

Введение

Возбуждение сейсмических вибрационных колебаний всегда сопровождается появлением кратных частот, которые обычно для краткости принято называть гармониками. Известно много способов их устранения, однако намного реже они используются для извлечения дополнительной информации о глубинном строении изучаемой среды. Возникновение гармоник связано как с условиями контакта вибрационной плиты с грунтом, так и с конструктивными особенностями самой виброустановки. Следовательно, они появляются в пункте возбуждения колебаний, после чего, наряду с основным свипом, распространяются в глубь среды и, претерпев отражение от глубинных неоднородностей, возвращаются назад к свободной поверхности, где регистрируются. Гармоники характеризуются более широким, чем у основного сигнала, частотным диапазоном, поэтому они могут быть использованы для повышения разрешенности сейсмической записи. Для этого следует предварительно отделить запись, связанную с сигналом, от записей, связанных с гармониками. Задачу успешно решает предложенный ранее алгоритм оптимизационной рекурсивной фильтрации [1], который, однако, разработан только для линейно-частотно-модулированных (ЛЧМ) сигналов. Позже он был обобщен на случай амплитудной модуляции и нелинейной частотной модуляции, после чего использован для расширения спектра сейсмической записи [2].

Достаточно полный обзор литературы, посвященной проблеме разделения сигнала и гармоник с возможным последующим использованием последних, приведен в статье [3]. Здесь мы дополним его свежими публикациями, в которых предлагается извлекать содержащуюся в кратных частотах полезную информацию. В работе [4] показано, как гармоники могут быть использованы для расширения частотного состава сигнала в верхней части разреза (ВЧР) при морской сейсморазведке с вибрационным источником. Авторы исследования [5] применяют разделение основного свипа и его гармоник на записи сигнала толкающего усилия (в англоязычной литературе — ground force) в области преобразования Габора (его аналог — спектрально-временной анализ (СВАН) или, оно же, спектрально-временное представление (СВП)), используя инверсионный подход. Затем к исходной виброграмме применяется корреляция отдельно по свипу и гармоникам. В работе [6] предлагается использовать так называемую скользящую фильтрацию (полосовая фильтрация с переменной по временной координате полосой пропускания) для разделения сигнала и гармоник на виброграммах. После этого можно коррелировать виброграммы с теоретическим свипом соответствующей гармоники и получать как коррелограммы, так и разрезы [7]. Такой подход способен корректно разделить сигнал и гармоники только для ВЧР, а отражения от глубинных горизонтов претерпевают частотные искажения. Авторы исследования [8] предлагают применять непрерывное вейвлет-преобразование для разделения сигнала и гармоник по данным ВСП. Как и в предыдущих подходах, методика корректно обрабатывает только отражения от горизонтов в ВЧР. После этого производится раздельное построение разрезов. Алгоритм удаления гармоник, ориентированный на обработку данных, полученных по методике slip-sweep [9], и основанный на различии формы импульсов сигнала и гармоники, предложен в [10].

Модель

Введенная в работе [11] модель дискретного вибросейсмического сигнала q(t) записывается в виде

$q(t)=∑_{m=1}^Ma_m (t)* q_m (t),$ (1) $q(t)=∑_(m=1)^M▒〖a_m (t)*〗 q_m (t)$

где $q_m (t)$ — m-я гармоника, $a_m (t)$ — фильтры, M — общее число гармоник, t — индекс дискретного времени. Звездочка обозначает свертку. Функцию $q_1 (t)$ (она же — теоретический, или опорный свип) мы называем сигналом основного тона, или первой гармоникой, при этом $a_1 (t)≡δ(t)$ — дискретная дельта-функция. Выражение (1) описывает разложение сигнала $q(t)$ по системе базисных функций, в роли которых выступают фильтрованные гармоники.

Все сигналы, с которыми приходится иметь дело при решении практических задач, являются так называемыми квазигармоническими функциями, т. е. описываются формулой $g (t) sin⁡(tf (t))$ , где $f (t)$ — мгновенная частота, $g (t)$ — огибающая. Помимо ЛЧМ, существует много вариантов нелинейно-частотно-модулированных, а также амплитудно- и нелинейно-частотно-модулированных сигналов.

Виброграмма $v(t)$ записывается в соответствии с традиционной сверточной моделью

$v (t) =r (t) *p(t)*q (t)$ $v(t)=r(t)*p(t)*q(t)$ (2),

где $r(t)$ — последовательность коэффициентов отражения, $p(t)$ — оператор, описывающий влияние на сигнал эффектов при прохождении ВЧР.

Прогнозирование гармоник

Рассмотрим способы расчета гармоник в зависимости от имеющейся в наличии априорной информации.

1. Если мгновенная частота задана в виде функции $f(t)$ , то вычисление гармоники m-го порядка не представляет сложности и производится в соответствии с выражением

$q_m (t)=g(t)sin⁡(tmf(t)).$

2. Если в распоряжении имеется запись толкающего усилия, то на ней гармоники наблюдаются одновременно с сигналом основного тона. Их можно разделить при помощи нестационарной полосовой фильтрации с оператором, частотный диапазон пропускания которого настраивается по СВАН-колонке записи толкающего усилия.

3. Если мгновенная частота не задана в явном виде и не записан сигнал толкающего усилия, гармоники можно спрогнозировать при помощи нелинейных формул, основанных на тригонометрических равенствах. Пусть в некоторый момент времени $t=t ̂$ мгновенная частота равна $f ̂=f(t ̂ )$ . Тогда в малой $ε$ -окрестности $t∈(t ̂-ε,t ̂+ε)$ основной свип записывается как $g(t ̂)sin⁡(tf(t ̂ ))$ и требуется разработать способ его пересчета в $g (t ̂) s i n (t m f (t ̂)).$ С этой целью используем тригонометрическое равенство

$sin^2 x=\frac{1-cos2x}{2}$ ,

а для гармоники третьего порядка

$sin^3 x=\frac{3sinx-sin3x}{4}$ .

Для сохранения правильной динамики гармоник следует также учитывать огибающую $g(t)$ . Действительно, каждая частотная компонента гармоники должна наследовать амплитуду, которую она имела в свипе основного тона. Следовательно, для записанных выше выражений требуется ввести коэффициент d, предполагая, что вместо $sinx$ регистрируется $dsinx$ .

Умножив обе части тригонометрического равенства, прогнозирующего вторую гармонику, на d², получим

$(dsinx)^2=d^2 \frac {1-2cosx}{2}$ ,

откуда следует

$dcosx=d-\frac{2(dsinx)^2}{d}$ .

В выписанных формулах вместо $dsinx$ следует подставлять $q_1 (t)$ , а вместо $dsin2x$ подставлять $q_2 (t)$ . Тогда приходим к преобразованию

$\frac{∂q_2 (t)}{∂t}=\frac{g(t)}{2}-\frac{q_1^2 (t)}{g(t)}$ .

Дифференцирование в левой части последнего равенства означает поворот фазы сигнала на $π⁄2$ . Таким образом, получаем окончательное выражение

$q_2 (t)=(\frac{g(t)}{2}-\frac{q_1^2 (t)}{g(t) })*l(t)$ ,

где $l(t)$ — оператор поворота фазы.

Если провести аналогичные рассуждения для третьей гармоники, получим

$q_3 (t)=3q_1 (t)-\frac{4}{g^2 (t)} q_1^3 (t)$ .

Разделение сигнала и гармоник

Преобразование виброграммы $v(t)$ в коррелограмму $z_1 (t)$ реализуется как корреляция $v(t)$ с $q_1 (t)$ (она же — свертка с инвертированной по временной оси функцией $q_1 (-t)$

$z_1 (t)=v(t)*q_1 (-t)$ (3).

Нижний индекс 1 указывает на то, что корреляцию можно применять не только по свипу первой гармоники, но и по свипам старших гармоник. Подставив (1) и (2) в (3), получим

$z_1 (t)=r(t)*p(t)*(c_11 (t)+∑_{m=2}^Ma_m (t)* c_{m1} (t))$ ,

где $c_{m1} (t)$ — функция взаимной корреляции (соответствующим образом определенная для детерминированных сигналов) первой и m-й гармоник: $c_{m1} (t)=q_m (t)*q_1 (-t)$ , а $c_11 (t)$ $c_11 (t)$ — автокорреляционная функция (АКФ) первой гармоники: $c_11 (t)=q_1 (t)*q_1 (-t)$ . Идеальная коррелограмма $z_1^{(ид)} (t)$ , на которой подавлены гармоники, записывается как

$z_1^{(ид)} (t)=r(t)*p(t)*c_11 (t)$ .

Тогда оператор, преобразующий исходную коррелограмму в желаемую, имеет спектральную характеристику

$L(ω)=\frac{Z_1^{(id)} (ω)}{Z_1 (ω)}$ .

Здесь и ниже заглавные буквы обозначают спектральные характеристики соответствующих функций, обозначенных прописными буквами. Таким образом,

$L(ω)=(1+∑_{m=2}^M\frac{A_m (ω) C_{m1} (ω)}{C_11 (ω)})^{-1}$ .

Для применения этого оператора требуется получить оценку спектральной характеристики $A_m (ω)$ , что реализуется при помощи оптимизационной процедуры, предложенной в работах [1, 12]. Входящие в последнее выражение функции $C_11 (ω)$ и $C_{m1} (ω)$ вычисляются на основании преобразований, выписанных в предыдущем разделе.

Выделив виброграмму, связанную только со свипом первой гармоники, вычтем ее из исходной виброграммы, чтобы получить набор данных, связанный только с гармониками старших порядков. Повторим все описанные выше расчеты для выделения гармоники второго порядка. Аналогичным образом выделим виброграммы остальных гармоник вплоть до максимального выбранного порядка. Затем применим корреляцию каждой виброграммы с соответствующим ей свипом, после чего получим набор коррелограмм, по которым построим временные разрезы.

Примеры

Результаты разделения сигнала и гармоник, а также использования гармоник для расширения спектра демонстрируются на коррелограммах и суммарных разрезах. После разделения были получены отдельные наборы данных, относящиеся к первой и второй гармоникам. К каждому из них применена корреляция со свипом соответствующей гармоники.

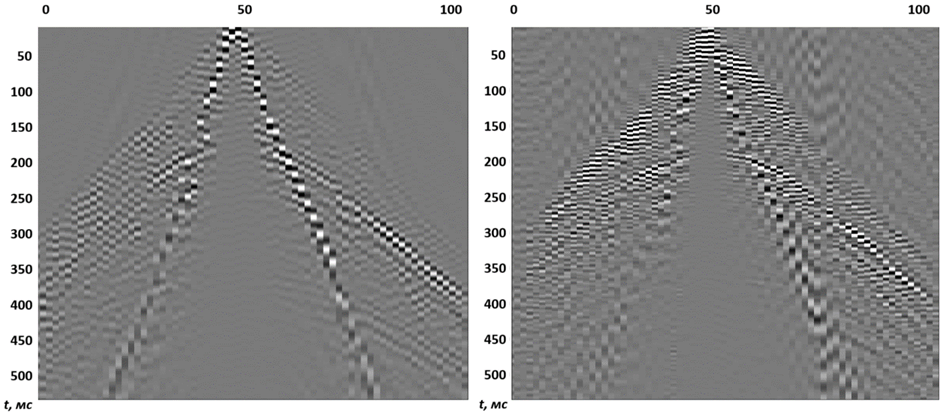
Рисунок 1. Коррелограммы, полученные после разделения сигнала и гармоник: слева — первой гармоники, справа — второй гармоники. По горизонтальной оси отложены условные номера пикетов общей средней точки (ОСТ)

Рисунок 2. Фрагмент разреза, полученный по коррелограммам: вверху — первой гармоники, внизу — второй гармоники. По горизонтальной оси отложены условные номера пикетов ОСТ

Данные были обработаны следующим образом: ввод геометрии, удаление случайных шумов (медианный фильтр в пространственно-частотной области), автоматическая регулировка усиления в окне длиной во всю трассу, расчет и применение короткопериодных статических поправок. На рисунке 1 показаны коррелограммы первой и второй гармоник (после разделения), здесь на качественном уровне можно увидеть различие одного и того же отражения на 200 мс. На рисунке 2 сравниваются временные разрезы первой и второй гармоник. Заметно существенное увеличение разрешенности волновой картины на разрезе второй гармоники. Наиболее явно это проявляется там, где на разрезе первой гармоники прослеживается только одно отражение, а на второй гармонике наблюдается сложная слоистая структура со складками и разломами. Напомним, что разрешающая способность сигнала пропорциональна ширине частотного диапазона, в котором сконцентрирована его спектральная характеристика. Эффект повышения разрешенности напоминает привычный эффект от деконволюции, однако понятно, что средствами обратной фильтрации не удастся так расширить спектр сигнала первой гармоники, чтобы насытить его спектральными компонентами вне диапазона частот возбуждения основного свипа (амплитудные спектры и оценки АКФ приведены соответственно на рисунках 3 и 4). Параметры свипа были выбраны следующим образом: полоса частот: 5–90 Гц, длина 32 с. Таким образом, никакие линейные преобразования сигнала не смогут добавить к его спектральной характеристике частоты выше 90 Гц. Применение деконволюции может расширить спектр трассы, но только за счет повышения уровня помехи.

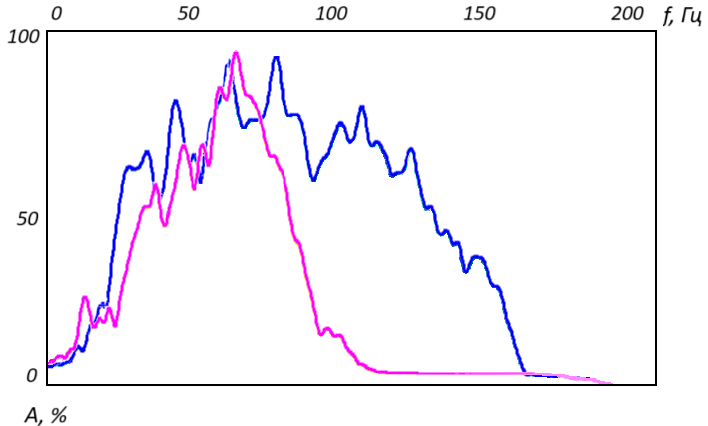
Рисунок 3. Амплитудные спектры разрезов (в линейном масштабе): голубая кривая — первой гармоники, пурпурная кривая — второй гармоники. По вертикальной оси отложены относительные амплитуды. Частота Найквиста равна 250 Гц, показан фрагмент спектра в диапазоне от 0 до 200 Гц. Выше 200 Гц обе спектральные характеристики стремятся к нулю

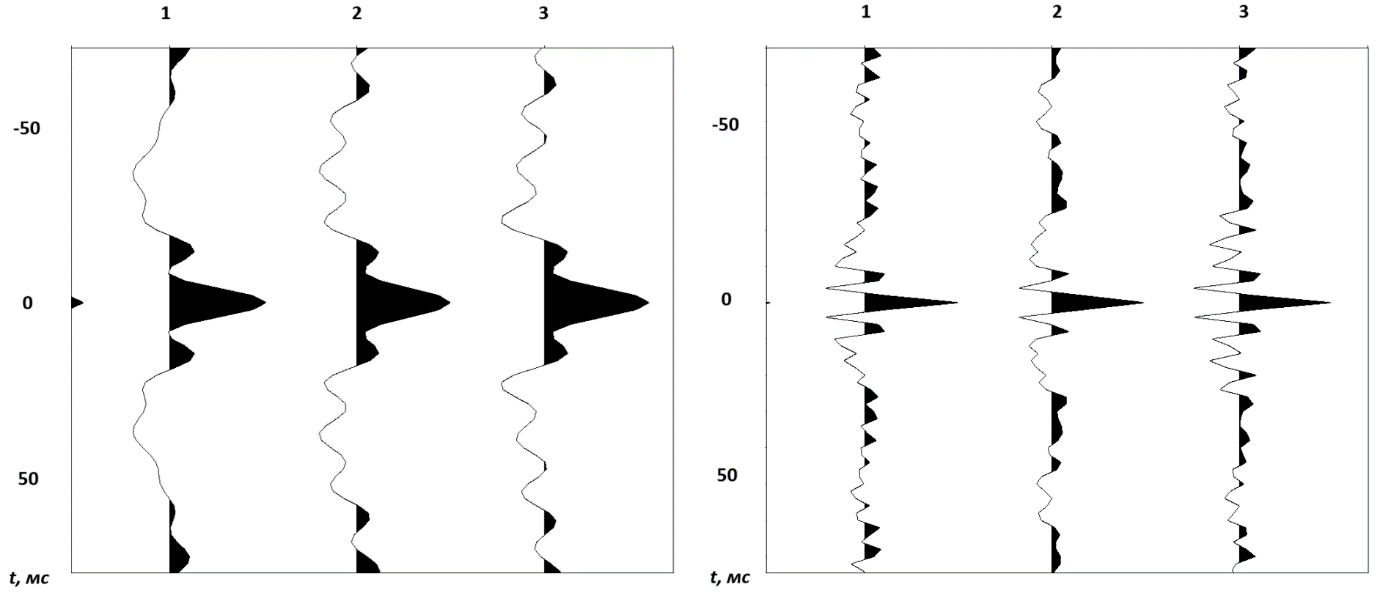
Рисунок 4. АКФ трех трасс, полученных после обработки: слева — первой гармоники, справа — второй гармоники. По горизонтальной оси отложены условные номера пикетов ОСТ

Количественное оценивание разрешенности волновой картины связано с известными трудностями. Здесь мы демонстрируем лишь эффект расширения амплитудного спектра импульса, который, как правило, приводит к повышению его разрешающей способности. Этот же эффект означает большую концентрацию энергии АКФ вокруг ее центрального значения. На рисунке 4 показаны нормированные оценки АКФ, полученные по разрезам основного свипа и второй гармоники. Последняя характеризуется лучшей фокусировкой. Впрочем, считаем необходимым вновь подчеркнуть, что сжатость АКФ может вовсе не свидетельствовать о сжатости импульса. В самом деле, в АКФ отсутствует информация о фазовом спектре импульса. Можно сказать, что АКФ инвариантна относительно фазы сигнала. В то же время именно фазовый спектр в первую очередь определяет разрешающую способность сигнала. Так, в книге [13] показано, что эффективная длина импульса пропорциональна максимальному значению модуля второй производной его фазового спектра, т. е. максимальной кривизне фазочастотной характеристики.

Рисунок 5. Увеличенный фрагмент разреза, полученного по коррелограммам: слева — первой гармоники, справа — второй гармоники. По горизонтальной оси отложены условные номера пикетов ОСТ

На рисунке 5 показан увеличенный фрагмент из левой части разреза, изображенного ранее на рисунке 2. В отличие от разреза первой гармоники, на разрезе второй гармоники можно детально рассмотреть тонкую слоистость отражающей пачки, различные складки, а также события, напоминающие дизъюнктивные нарушения по краям объекта. Этот же фрагмент волновой картины показан на рисунке 6 с использованием цветокодированной палитры, которая позволяет лучше проинтерпретировать некоторые детали волновых полей.

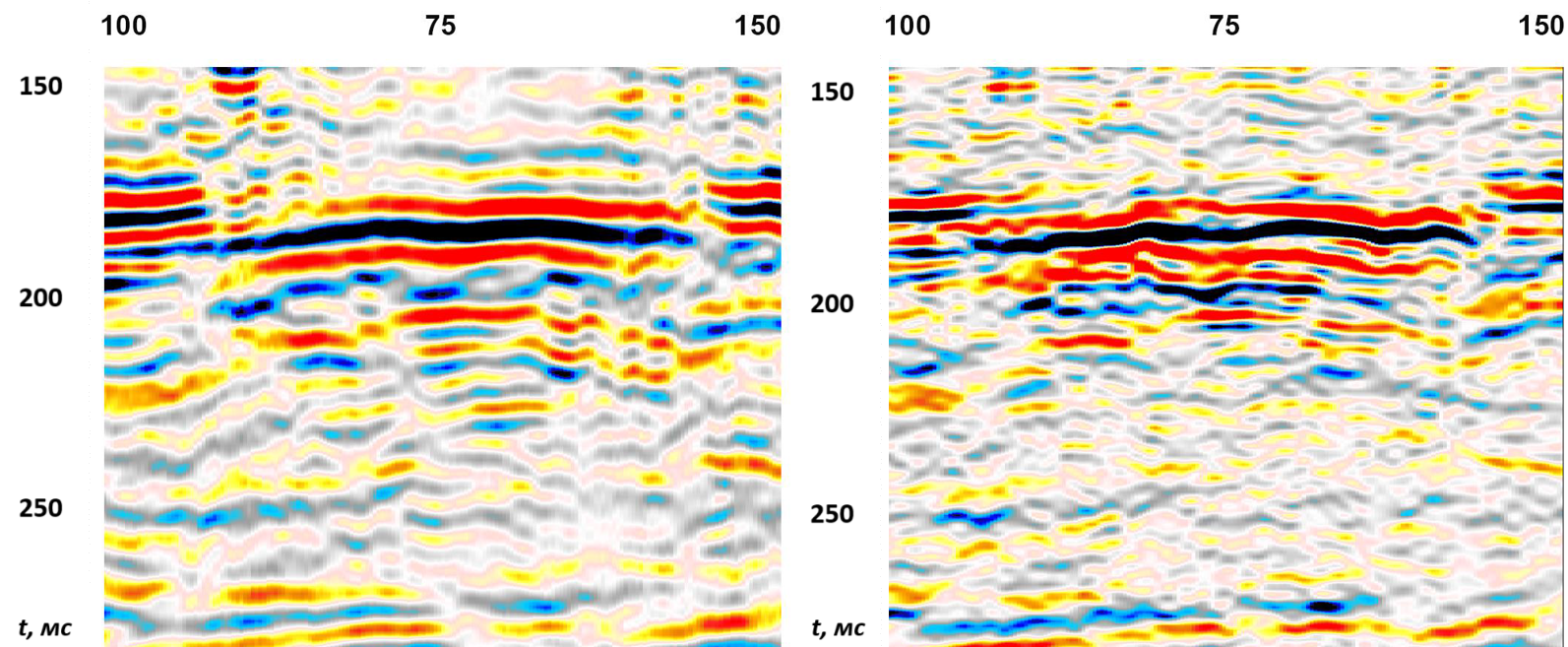
Рисунок 6. Увеличенный фрагмент разреза, полученного по коррелограммам, показанный в цветокодированной палитре: слева — первой гармоники, справа — второй гармоники. По горизонтальной оси отложены условные номера пикетов ОСТ

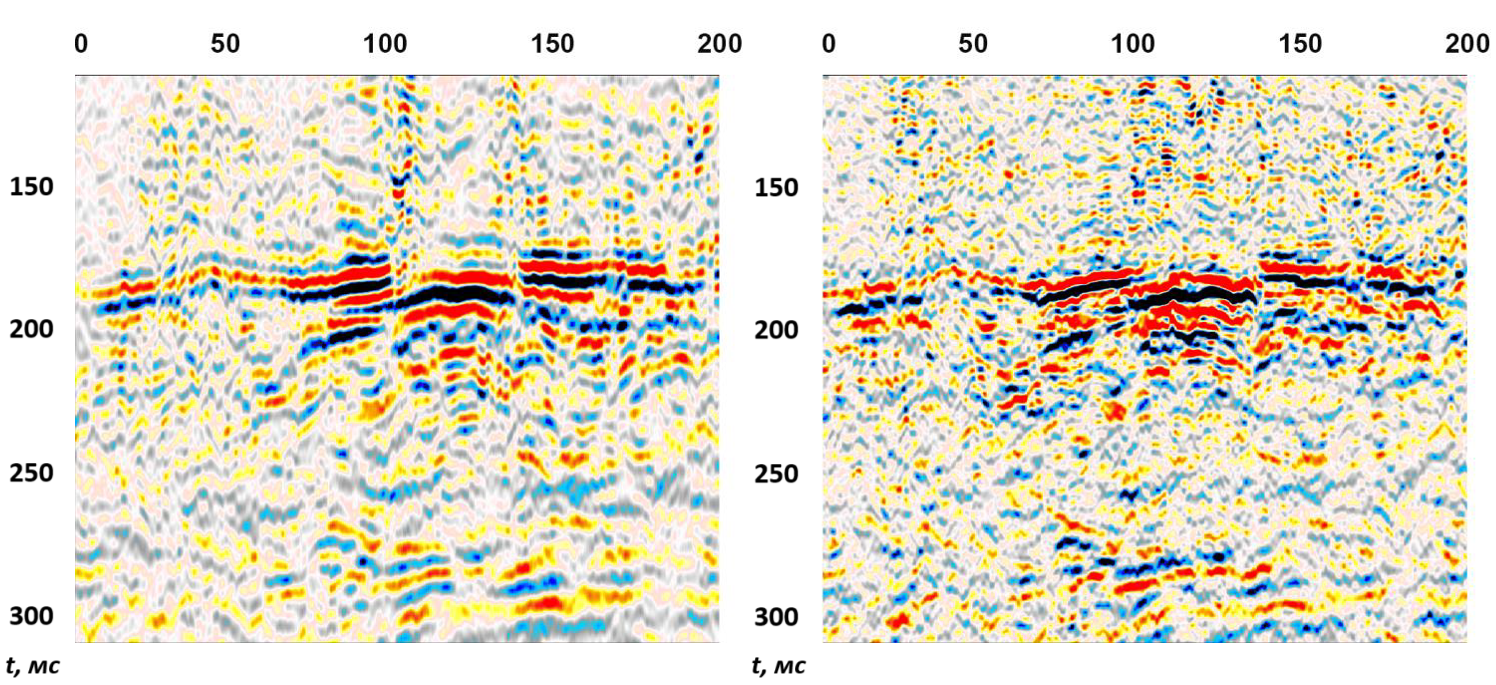
Рисунок 7. Увеличенный фрагмент разреза, полученного по коррелограммам, показанный в цветокодированной палитре: слева — первой гармоники, справа — второй гармоники. По горизонтальной оси отложены условные номера пикетов ОСТ

На рисунке 7 представлен увеличенный фрагмент разреза, из анализа которого следует, что разрешающая способность заметно увеличилась и на других пространственно-временных интервалах. Разрез второй гармоники оказывается насыщенным деталями, которые отсутствуют на разрезе первой гармоники, и это позволяет провести более тщательную его интерпретацию.

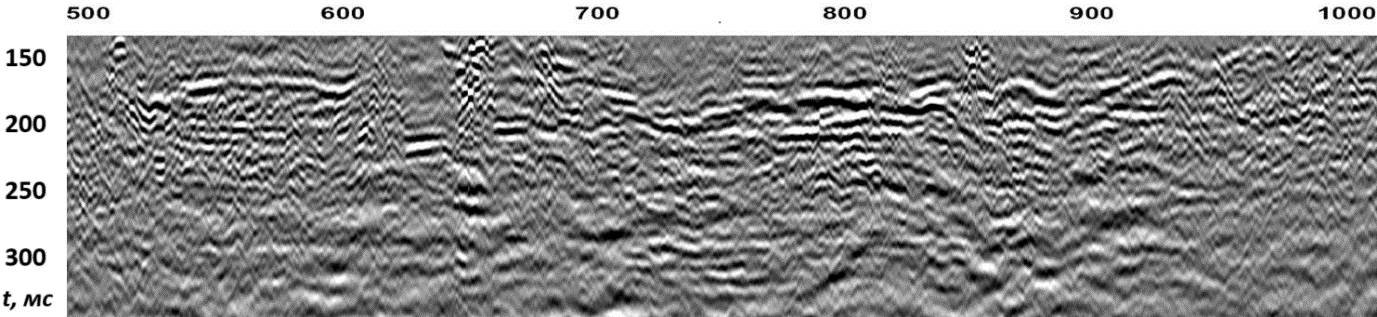
Рисунок 8. Фрагмент разреза, полученного по коррелограммам: вверху — первой гармоники, внизу — второй гармоники. По горизонтальной оси отложены условные номера пикетов ОСТ

На рисунке 8 показан увеличенный фрагмент из правой части разреза, изображенного на рисунке 2. Различия волновых картин прежние. Вновь разрез второй гармоники имеет лучшую разрешенность и оказывается насыщенным деталями, которые не проявлялись на разрезе первой гармоники.

Показанные на рисунках фрагменты разрезов относятся к ВЧР. В самом алгоритме не заложено никаких ограничений на глубинность, и его использование теоретически позволяет получать сигнал с расширенным спектром на всем временном интервале регистрации колебаний. Имеющийся в нашем распоряжении набор полевых виброграмм, к сожалению, характеризуется весьма малым уровнем энергии гармоник старших порядков. Если в среднем суммарный уровень всех гармоник достигает 20–30 % уровня сигнала [14], то в использованных нами виброграммах этот уровень ограничен лишь величиной 5–6 %. Кроме того, в данных сейсмогеологических условиях наблюдается значительное затухание энергии высокочастотной части спектра в пределах ВЧР. Поэтому выделение сигнала второй гармоники для средней и нижней частей разреза малоэффективно. Если сравнивать нижние части разрезов, полученных по основному свипу и второй гармонике, то отличия будут малозаметными.

Выводы

Мы кратко изложили основные принципы алгоритма оптимизационной рекурсивной фильтрации, обобщенного на случай нелинейной частотной, а также амплитудной модуляции. Этот алгоритм отделяет сейсмограмму, связанную с сигналом основного тона, от сейсмограмм, связанных с гармониками, а также отделяет сейсмограммы гармоник различного порядка друг от друга. После такого разделения волновых полей возможно построение временных разрезов по соответствующим коррелограммам.

Работоспособность алгоритма подтверждается примерами обработки полевых данных. За счет использования второй гармоники удалось почти вдвое расширить спектр и, как следствие, значительно повысить разрешенность записи.

Пока мы ограничились совместной интерпретацией разрезов основного тона и гармоник. В дальнейшем планируется решить задачу их суммирования с использованием критерия оптимальности, добиваясь наибольшего расширения спектра сигнала с учетом требования максимизации отношения сигнал/шум.

Показанные результаты получены для сигнала основного тона и второй гармоники. Если применить алгоритм разделения волновых полей, можно выделить и виброграммы гармоник старших порядков. Такие поля отличаются убывающим с ростом порядкового номера гармоники отношением сигнал/шум.

Полученные результаты обработки полевых виброграмм требуют верификации. Конечно же, геологическое подтверждение необходимо для результата любой процедуры обработки сейсмических данных, и это реализуется в процессе интерпретационного сопровождения, когда применяется привязка к скважинам. В данной ситуации мы работаем с формой сейсмического импульса и претендуем на то, чтобы расширить его амплитудный спектр. Именно этой цели мы достигли, подтвердив ее результатами спектрального оценивания. Скважинных данных на этом профиле не было. Алгоритм использует традиционную сверточную модель сейсмической трассы. Это линейная модель, и на ней основаны все методы фильтрации, в том числе обратной фильтрации. На основании этой модели мы извлекаем из виброграмм дополнительную информацию, которая теряется при традиционной корреляции. Сейсмические данные после предварительного применения к ним набора линейных процедур разделения сигналов подвергаются традиционной процедуре корреляции, но уже по свип-сигналу соответствующей гармоники. В этой особенности алгоритма мы видим одно из соображений, позволяющих утверждать, что он имеет собственные внутренние средства верификации полученных результатов.

Применение методики расширения спектра сигнала требует сохранения виброграмм, что не является препятствием с учетом компактности и доступности современных средств хранения больших массивов данных. Чтобы сохранить больше высокочастотных компонент, рекомендуется при регистрации колебаний выбирать меньший шаг дискретизации. Например, если верхняя частота диапазона возбуждения основного свипа равна 90 Гц, вторая гармоника займет диапазон частот до 180 Гц. Тогда, если выбрать шаг дискретизации 4 мс, которому соответствует частота Найквиста 125 Гц, значительная часть энергии второй гармоники будет утеряна.

В последнее время вновь возрождается интерес к задаче расширения спектра сигнала. В подавляющем большинстве работ используется принцип продолжения спектра в область вне частотного диапазона, который был зарегистрирован в процессе записи колебаний. Частотная характеристика трассы из зарегистрированного сигнального диапазона математически экстраполируется вне этого диапазона на низкие и высокие частоты. Понятно, что такая задача имеет более одного решения, и для того, чтобы получить некоторое решение, используют ту или иную априорную информацию о свойствах импульса и последовательности коэффициентов отражения. Соответствующие методики давно применяются при обработке сейсмических сигналов, а их обзор (применительно к более общей задаче обработки изображений) можно найти, например, в книге [15]. Недостатки методик также хорошо известны. Важно иметь в виду, что получаемые при помощи алгоритмов продолжения спектра частоты не были зарегистрированы в процессе наблюдений. Принято называть их «фантомными». Также понятно, что если применить два разных алгоритма, то и результаты будут, вообще говоря, разными. Принцип расширения спектра, которого мы здесь придерживаемся, основан на использовании только тех частот, которые были реально получены в процессе регистрации, и наш алгоритм решает задачу их выделения.

Список литературы

1. Денисов М. С. Оптимизационная рекурсивная фильтрация как способ подавления гармоник в методе вибросейс / Денисов М. С., Егоров А. А. // Геофизические технологии. — 2019. — № 2. — С. 23–53. — https://doi.org/10.18303/2619-1563-2019-2-23.

2. Денисов М. С. Использование гармоник вибросейсмических амплитуд-но- и нелинейно- частотно модулированных сигналов для расширения спектра сейсмической записи / Денисов М. С., Зыков А. А. // 26-я науч-но-практическая конференция по вопросам геологоразведки и разработ-ки месторождений нефти и газа Геомодель 2024: сборник тезисов. — С. 106–110.

3. Денисов М. С. Optimization-based recursive filtering for separation of sig-nal from harmonics in Vibroseis / Денисов М. С., Егоров А. А., Shneerson M. B. // Geophysical Prospecting. — 2021. — Т. 69. — № 4. — С. 779–798. — https://doi.org/10.1111/1365-2478.13084.

4. Wang T. Extending seismic bandwidth using the harmonic energy of a ma-rine vibrator source / Wang T., JafarGandomi A., Aune H. // 3rd International Meeting for Applied Geoscience and Energy (SEG 2023): Expanded Ab-stracts. — С. 177–181. — https://doi.org/10.1190/image2023-3909863.1.

5. Caporal M. Automated, inversion-based fundamental and higher order har-monics separation / Caporal M., Tsingas C., Almubarak M. S., Alnasser H. // 83rd EAGE Annual Conference and Exhibition: Expanded Abstracts. — 2022. — С. 1–5. — https://doi.org/10.3997/2214-4609.202210032.

6. Ягудин И. Р. Нелинейные искажения как дополнительный источник сейсмической информации в вибрационной сейсморазведке / Ягудин И. Р., Гафаров Р. М., Жужель А. С. // 26-я научно-практическая конфе-ренция по вопросам геологоразведки и разработки месторождений нефти и газа Геомодель 2024: сборник тезисов. — С. 129–132.

7. Ягудин И. Р. Нелинейные искажения как дополнительный источник сейсмической информации в вибрационной сейсморазведке / Ягудин И. Р., Гафаров Р. М., Жужель А. С. // Приборы и системы разведочной геофизики. — 2024. — № 3. — С. 16–22.

8. Alnasser H. Fundamentals and higher order harmonics separation and inte-gration from vertical seismic profiling (VSP) data / Alnasser H., Shaiban A., El Yadari N., Almarzooq M. // 82nd EAGE Annual Conference and Exhibition: Expanded Abstracts. — 2021. — С. 1–5. — https://doi.org/10.3997/2214-4609.202113038.

9. Rozemond H. J. Slip-sweep acquisition / Rozemond H. J. // 66th SEG Annu-al Meeting and Exposition: Expanded Abstracts. — 1996. — С. 64–67. — https://doi.org/10.1190/1.1826730.

10. Liu D. Eliminating harmonic noise in vibrator data through sparsity-promoted waveform modeling / Liu D., Li X., Wang W., Wang X., Shi Z., Chen W. // Geophysics. — 2022. — Т. 87. — № 3. — С. V183 – V191. — https://doi.org/10.1190/geo2021-0448.1.

11. Денисов М. С. Построение модели вибросейсмического сигнала, осложненного гармониками / Денисов М. С., Егоров А. А. // Геофизиче-ские технологии. — 2019. — № 1. — С. 72–83. — https://doi.org/10.18303/2619-1563-2019-1-72.

12. Денисов М. С. Разделение. сигнала и гармоник в невзрывной сейсмо-разведке с амплитудно и нелинейно частотно-модулированными сиг-налами / Денисов М. С., Зыков А. А. // Геофизические технологии. — 2023. — № 3. — С. 69–83. — https://doi.org/10.18303/2619-1563-2023-3-69.

13. Варакин Л. Е. Теория сложных сигналов / Варакин Л. Е. — М.: Совет-ское радио, 1970.

14. Ведерников Г. В. Исследование кратных гармоник вибросигналов / Ве-дерников Г. В., Максимов Л. А., Жарков А. В. // Геофизика. Спецвыпуск к 30-летию «Сибнефтегеофизики». — 2001. — С. 33–38.

15. Василенко Г. И. Восстановление изображений / Василенко Г. И., Тара-торин А. М. — Москва: Радио и связь, 1986.

Отправить рукопись Скачать PDF
Текст JATS XML